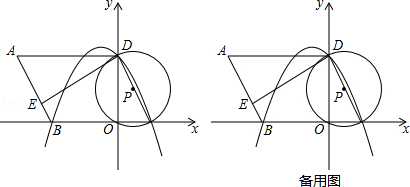��Ŀ����
����Ŀ��̽�����ɣ�
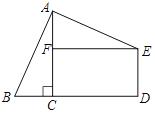
��1����ͼ1����֪��ABCΪֱ�������Σ���A=90�㣬����ͼ������ȥ��A�� ���1+��2����
A.90�� B.135�� C.270�� D.315��
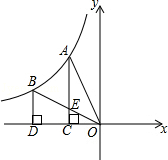
��2����ͼ2����֪��ABC�У���A=40�㣬��ȥ��A����ı��Σ����1+��2=
��3����ͼ2�����ݣ�1���루2���������̣�������ɲ����1+��2���A�Ĺ�ϵ��
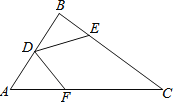
��4����ͼ3����û�м��������ǰ����۳���ͼ3��״����̽����1+��2���A�Ĺ�ϵ��˵�����ɣ�

���𰸡���1�����ı��ε��ڽǺ�Ϊ360����ֱ����������������Ǻ�Ϊ90��
���1+��2=360��-����A+��B��=360��-90��=270����
���1+��2����270����C��
��2����1+��2=180��+40��=220����220����
��3����1+��2=180��+��A��
��4������һ:�ߡ�EFP������EFA�۵��õ���
���AFE=��PFE����AEF=��PEF
���1=180��-2��AFE����2=180��-2��AEF
���1+��2=360��-2����AFE+��AEF��
���ߡ�AFE+��AEF=180��-��A
���1+��2=360��-2��180��-��A��=2��A
������: �ߡ�1+��PFE=��AEF+��A, ��2+��PEF=��AFE+��A
���1+��PFE+��2+��PEF=��AEF+��AFE+2��A
�ߡ�EFP������EFA�۵��õ���
���AFE=��PFE����AEF=��PEF
���1+��2=2��A
��������
(1)�����������ı����ڽǺ�Ϊ360����ֱ�������ε�������⣻
(2) ���������ε���ǵ������������ڵ������ڽǺ���⣻
(3)���ݣ�1������2�����ɳ����ۣ�
(4) ������Ҫ��ͼ����������ȵ�����ͼ1��DEΪ�ۺۣ�����A=��DA��A����������ǵ����ʿɵý�����BDA��=2��Aͼ2����A����DA��E����ȵģ��ٽ���ı��ε��ڽǺͼ������ǵ����ʿɵý�����BDA��+��CEA��=2��Aͼ3�������۵���A����DA��E����ȵģ�������������������ǵ����ʿɵý��ۣ�

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�����Ŀ������������6000Ԫ�����ס���������Ʒ����������Ʒ�ļ����ȼ���Ʒ������![]() ��15�����ס���������Ʒ�Ľ��ۺ��ۼ����±�����ע���������ۼ۩����ۣ�
��15�����ס���������Ʒ�Ľ��ۺ��ۼ����±�����ע���������ۼ۩����ۣ�
�� | �� | |
���ۣ�Ԫ/���� | 22 | 30 |
�ۼۣ�Ԫ/���� | 29 | 40 |
��1�����̳������ס���������Ʒ�����ټ���
��2���ó��н������ļס���������Ʒȫ�������һ���ɻ�ö�������