题目内容
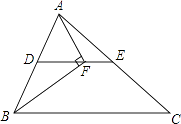
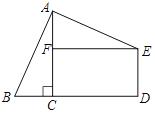
【题目】在Rt△ABC中,∠ACB=90°,BC=5,过点A作AE⊥AB且AB=AE,过点E分别作EF⊥AC,ED⊥BC,分别交AC和BC的延长线与点F、D.
(1)求证:△ABC≌△EAF;
(2)若FC=7,求四边形ABDE的周长.
【答案】(1)见解析;(2)50
【解析】
(1)根据AAS证明△ABC≌△EAF即可;
(2)由全等三角形的性质得出BC=AF,AC=EF,再利用勾股定理得出AB的长,进而得出四边形EFCD是矩形,求出四边形ABDE的周长即可;
(1)证明:∵∠ACB=90°,AE⊥AB,
∴∠1+∠B=∠1+∠2=90°,
∴∠B=∠2,
∵EF⊥AC,
∴∠4=∠5=90°,
∴∠3=∠4,
在△ABC和△EAF中,
 ,
,
∴△ABC≌△EAF(AAS).
(2)解:∵△ABC≌△EAF
∴BC=AF,AC=EF,
∵BC=5,
∴AF=5,
∵FC=7,
∴AC=EF=12,
在Rt△ABC中,AB=![]() =13,
=13,
∴AE=AB=13,
∵ED⊥BC,
∴∠7=∠6=∠5=90°,
∴四边形EFCD是矩形,
∴CD=EF=12,ED=FC=7,
∴四边形ABDE的周长=AB+BD+DE+EA=13+5+12+7+13=50.

【题目】为了保护环境,某校环保小组成员小明收集废电池,第一天收集1号电池4节,5号电池5节,总质量为450克;第二天收集1号电池2节,5号电池3节,总质量为240克.
(1)求1号电池和5号电池每节分别重多少克;
(2)学校环保小组为估算四月份收集废电池的总质量,他们随机抽取了该月某5天每天收集废电池的数量,如下表:
1号废电池数量/节 | 29 | 30 | 32 | 28 | 31 |
5号废电池数量/节 | 51 | 53 | 47 | 49 | 50 |
分别计算收集的两种废电池数量的样本平均数,并由此估算该月环保小组收集废电池的总质量是多少千克;
(3)试说明上述表格中数据的获取方法是抽样调查还是全面调查,你认为这种方法合理吗?