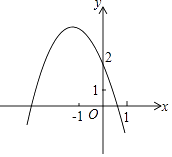��Ŀ����
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�OΪԭ�㣬ƽ���ı���ABCD�ı�BC��x���ϣ�D����y���ϣ�C������Ϊ��2��0����BC=6����BCD=60�㣬��E��AB��һ�㣬AE=3EB����P��D��O��C���㣬������y=ax2+bx+c����D��B��C���㣮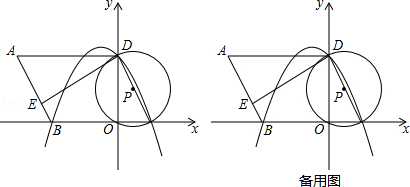
��1���������ߵĽ���ʽ��
��2��˵��ED�ǡ�P�����ߣ�������ADE�Ƶ�D��ʱ����ת90�㣬E��Ķ�Ӧ��E�������������������˵�����ɣ�
��3������MΪ�������ߵĶ��㣬ƽ�����Ƿ���ڵ�N��ʹ���Ե�B��D��M��NΪ������ı���Ϊƽ���ı��Σ������ڣ���ֱ��д����N�����ꣻ�������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺��C������Ϊ��2��0����BC=6��
��B����4��0����
��Rt��OCD����tan��OCD= ![]() ��
��
��OD=2tan60��=2 ![]() ��
��
��D��0��2 ![]() ����
����
�������ߵĽ���ʽΪy=��x+4����x��2����
��D��0��2 ![]() �������a4����2��=2
�������a4����2��=2 ![]() ��
��
��ã�a=�� ![]() ��
��
�������ߵĽ���ʽΪy=�� ![]() ��x+4����x��2��=��
��x+4����x��2��=�� ![]() x2��
x2�� ![]() x+2
x+2 ![]()
��2��
�⣺��Rt��OCD�У�CD=2OC=4��
���ı���ABCD��ƽ���ı��Σ�
��AB=CD=4��AB��CD����A=��BCD=60�㣬AD=BC=6��
��AE=3BE��
��AE=3��
�� ![]() ��
�� ![]() =
= ![]() =
= ![]() ��
��
�� ![]() ��
��
�ߡ�DAE=��DCB��
���AED�ס�DCB��
���ADE=��CDO��
�ߡ�ADE+��ODE=90�㣬
���CDO+��ODE=90�㣬
��CD��DE��
�ߡ�DOC=90�㣬
��CDΪ��P��ֱ����
��ED�ǡ�P�����ߣ�
E��Ķ�Ӧ��E�䲻�������������ϣ�
���ɣ��ߡ�AED�ס�COD��
�� ![]() ��
��
�� ![]() =
= ![]() ��
��
��ã�DE=3 ![]() ��
��
�ߡ�CDE=90�㣬DE��DC��
�ཫ��ADE�Ƶ�D��ʱ����ת90�㣬E��Ķ�Ӧ��������DC�ϣ�����D��C���������ϣ�
���E�䲻������������
��3��
�⣺���ڣ���y=�� ![]() x2��
x2�� ![]() x+2
x+2 ![]() =��
=�� ![]() ��x+1��2+
��x+1��2+ ![]() ��
��
��M����1�� ![]() ����
����
��B����4��0����D��0��2 ![]() ����
����
��ͼ����BMΪƽ���ı���BDMN�ĶԽ���ʱ��
��D����ƽ��4����λ��������ƽ��2 ![]() ����λ�õ�B��
����λ�õ�B��
���M����1�� ![]() ������ƽ��4����λ��������ƽ��2
������ƽ��4����λ��������ƽ��2 ![]() ����λ�õ�N1����5��
����λ�õ�N1����5�� ![]() ����
����
��DMΪƽ���ı���BDMN�ĶԽ���ʱ��
��B����ƽ��3����λ��������ƽ�� ![]() ����λ�õ�D��
����λ�õ�D��
���M����1�� ![]() ������ƽ��4����λ��������ƽ��2
������ƽ��4����λ��������ƽ��2 ![]() ����λ�õ�N2��3��
����λ�õ�N2��3�� ![]() ����
����
��BDΪƽ���ı���BDMN�ĶԽ���ʱ��
��M����ƽ��1����λ��������ƽ�� ![]() ����λ�õ�D��
����λ�õ�D��
���B����4��0������ƽ��1����λ��������ƽ�� ![]() ����λ�õ�N3����3����
����λ�õ�N3����3���� ![]() ����
����
�����������Ե�B��D��M��NΪ������ı���Ϊƽ���ı���ʱ����N������Ϊ����5�� ![]() ����3��
����3�� ![]() ����3����
����3���� ![]() ����
����
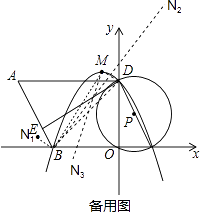
����������1����ֱ�������εõ�D��0��2 ![]() �����������ߵĽ���ʽΪy=��x+4����x��2������D��0��2
�����������ߵĽ���ʽΪy=��x+4����x��2������D��0��2 ![]() �����ɵõ����ۣ���2������ƽ���ı��ε����ʵõ�AB=CD=4��AB��CD����A=��BCD=60�㣬AD=BC=6���������������ε����ʵõ���ADE=��CDO�����ǵõ�CDΪ��P��ֱ�����������ߵ��ж������õ�ED�ǡ�P�����ߣ�E��Ķ�Ӧ��E�䲻�������������ϣ��������������ε���֪����DE=3
�����ɵõ����ۣ���2������ƽ���ı��ε����ʵõ�AB=CD=4��AB��CD����A=��BCD=60�㣬AD=BC=6���������������ε����ʵõ���ADE=��CDO�����ǵõ�CDΪ��P��ֱ�����������ߵ��ж������õ�ED�ǡ�P�����ߣ�E��Ķ�Ӧ��E�䲻�������������ϣ��������������ε���֪����DE=3 ![]() ��������ת����֪����E��Ķ�Ӧ��������DC�ϣ�����D��C���������ϣ����ǵõ���E�䲻�����������ϣ���3�����ݶ��κ����Ľ���ʽ�õ�M����1��
��������ת����֪����E��Ķ�Ӧ��������DC�ϣ�����D��C���������ϣ����ǵõ���E�䲻�����������ϣ���3�����ݶ��κ����Ľ���ʽ�õ�M����1�� ![]() ������B����4��0����D��0��2
������B����4��0����D��0��2 ![]() ������BMΪƽ���ı���BDMN�ĶԽ���ʱ����DMΪƽ���ı���BDMN�ĶԽ���ʱ����BDΪƽ���ı���BDMN�ĶԽ���ʱ������ƽ�Ƶ����ʼ��ɵõ����ۣ�
������BMΪƽ���ı���BDMN�ĶԽ���ʱ����DMΪƽ���ı���BDMN�ĶԽ���ʱ����BDΪƽ���ı���BDMN�ĶԽ���ʱ������ƽ�Ƶ����ʼ��ɵõ����ۣ�
�����㾫��������ƽ���ı��ε����ʺͽ�ֱ���������ǽ����ĸ�������Ҫ֪��ƽ���ı��εĶԱ������ƽ�У�ƽ���ı��εĶԽ���ȣ��ڽǻ�����ƽ���ı��εĶԽ�����ƽ�֣���ֱ�������ε����ݣ��ٱߵĹ�ϵa2+b2=c2���ڽǵĹ�ϵ��A+B=90�㣻�۱߽ǹ�ϵ�����Ǻ����Ķ��壮(ע�⣺��������ʹ���м����ݺͳ���)��

����Ŀ��Ϊ�˱�������,ijУ����С���ԱС���ռ��ϵ��,��һ���ռ�1�ŵ��4��,5�ŵ��5��,������Ϊ450��;�ڶ����ռ�1�ŵ��2��,5�ŵ��3��,������Ϊ240��.
(1)��1�ŵ�غ�5�ŵ��ÿ�ڷֱ��ض��ٿ�;
(2)ѧУ����С��Ϊ�������·��ռ��ϵ�ص�������,���������ȡ�˸���ij5��ÿ���ռ��ϵ�ص�����,���±�:
1�ŷϵ������/�� | 29 | 30 | 32 | 28 | 31 |
5�ŷϵ������/�� | 51 | 53 | 47 | 49 | 50 |
�ֱ�����ռ������ַϵ������������ƽ����,���ɴ˹�����»���С���ռ��ϵ�ص��������Ƕ���ǧ��;
(3)��˵���������������ݵĻ�ȡ�����dz������黹��ȫ�����,����Ϊ���ַ���������?