题目内容
【题目】如图，反比例函数y= 
（k≠0）的图象经过A，B两点，过点A作AC⊥x轴，垂足为C，过点B作BD⊥x轴，垂足为D，连接AO，连接BO交AC于点E，若OC=CD，四边形BDCE的面积为2，则k的值为 ． 
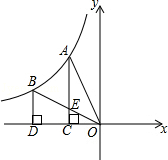
【答案】﹣ 
【解析】解：设点B坐标为（a，b），则DO=﹣a，BD=b ∵AC⊥x轴，BD⊥x轴
∴BD∥AC
∵OC=CD
∴CE= 
BD= b，CD= DO= 
a
∵四边形BDCE的面积为2
∴ （BD+CE）×CD=2，即 （b+ b）×（﹣ a）=2
∴ab=﹣
将B（a，b）代入反比例函数y= 
（k≠0），得
k=ab=﹣
故答案为：﹣ 
先设点B坐标为（a，b），根据平行线分线段成比例定理，求得梯形BDCE的上下底边长与高，再根据四边形BDCE的面积求得ab的值，最后计算k的值．
练习册系列答案
优学名师名题系列答案
相关题目
【题目】为了保护环境,某校环保小组成员小明收集废电池,第一天收集1号电池4节,5号电池5节,总质量为450克;第二天收集1号电池2节,5号电池3节,总质量为240克.
(1)求1号电池和5号电池每节分别重多少克;
(2)学校环保小组为估算四月份收集废电池的总质量,他们随机抽取了该月某5天每天收集废电池的数量,如下表:
1号废电池数量/节 | 29 | 30 | 32 | 28 | 31 |
5号废电池数量/节 | 51 | 53 | 47 | 49 | 50 |
分别计算收集的两种废电池数量的样本平均数,并由此估算该月环保小组收集废电池的总质量是多少千克;
(3)试说明上述表格中数据的获取方法是抽样调查还是全面调查,你认为这种方法合理吗?
