题目内容
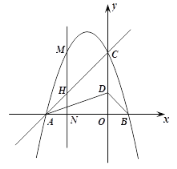
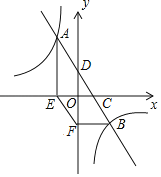
【题目】如图,已知一次函数y=﹣2x+b与反比例函数y=![]() 的图象有两个交点A(m,3)和B,且一次函数y=﹣2x+b与x轴、y轴分别交于点C、D.过点A作AE⊥x轴于点E;过点B作BF⊥y轴于点F,点F的坐标为(0,﹣2),连接EF,tan∠FEO=2.
的图象有两个交点A(m,3)和B,且一次函数y=﹣2x+b与x轴、y轴分别交于点C、D.过点A作AE⊥x轴于点E;过点B作BF⊥y轴于点F,点F的坐标为(0,﹣2),连接EF,tan∠FEO=2.
(1)求一次函数与反比例函数的解析式;
(2)求四边形AEFD的面积.
【答案】(1)一次函数的解析式为:y=-2x+1;反比例函数的解析式为:y=-![]() ;(2)3.
;(2)3.
【解析】
(1)先利用正切的定义计算出OE=1,从而得到A点坐标,然后把A点坐标分别代入y=-2x+b,y=![]() 中求出b和k,从而得到一次函数与反比例函数的解析式;
中求出b和k,从而得到一次函数与反比例函数的解析式;
(2)先确定D点坐标,然后利用S四边形AEFD=S梯形AEOD+S△FEO进行计算即可.
(1)∵点F(0,-2),
∴OF=2,
在Rt△OEF中,tan∠FEO=![]() =2
=2
∴OE=1,
∵AE⊥x,
∴点A(-1,3),
将点A(-1,3)分别代入y=-2x+b,y=![]() 得b=1,k=-3,
得b=1,k=-3,
∴一次函数的解析式为:y=-2x+1;
反比例函数的解析式为:y=-![]() ;
;
(2)当x=0时,y=-2x+1=1,则D(0,1),
∴S四边形AEFD=S梯形AEOD+S△FEO=![]() ×(1+3)×1+
×(1+3)×1+![]() ×1×2=3.
×1×2=3.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目