题目内容
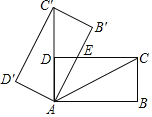
【题目】如图,将矩形ABCD绕点A旋转至矩形AB′C′D′位置,此时AC的中点恰好与D点重合,AB'交CD于点E,若AB=3cm,则线段EB′的长为_____.
【答案】1cm
【解析】
根据旋转后AC的中点恰好与D点重合,利用旋转的性质得到直角三角形ACD中,∠ACD=30°,再由旋转后矩形与已知矩形全等及矩形的性质得到∠DAE为30°,进而求出AD,DE,AE的长,则EB′的长可求出.
解:由旋转的性质可知:AC=AC',
∵D为AC'的中点,
∴AD=![]() AC,
AC,
∵ABCD是矩形,
∴AD⊥CD,
∴∠ACD=30°,
∵AB∥CD,
∴∠CAB=30°,
∴∠C'AB'=∠CAB=30°,
∴∠EAC=30°,
∴∠DAE=30°,
∵AB=CD=3cm,
∴AD=![]() cm,
cm,
∴DE=1cm,
∴AE=2cm,
∵AB=AB'=3cm,
∴EB'=3﹣2=1cm.
故答案为:1cm.

练习册系列答案
相关题目