Question

【题目】如图，正方形的边长为6，是边上的一点，绕点逆时针旋转后得到．三点在同一直线上．

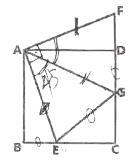
（1）求四边形的面积．

（2）如果点在边上，且，试判断之间有什么样的数量关系？并说明理由．

（3）在（2）的条件下，若，求的长．

Answer 1

【答案】（1）36；（2）GE＝DG＋BE，理由见解析；（3）的长为3．

【解析】

（1）由旋转的性质得△ABE≌△ADF，进而得出S四边形AECF＝S正方形ABCD，计算即可；

（2）根据旋转的性质求出∠GAF＝45°，然后利用SAS证明△AGE≌△AGF，得到GE＝GF，等量代换即可求出GE＝DG＋BE；

（3）设DG＝x，求出CG＝6－x，EC＝4，GE＝x+2，然后在Rt△CEG中利用勾股定理构建方程，求出x即可．

解：（1）由旋转的性质得：△ABE≌△ADF，

∴，

∴S四边形AECF＝S四边形AECD+S△ADF＝S四边形AECD+S△ABE＝S正方形ABCD＝6×6＝36；

（2）GE＝DG＋BE，

理由：由旋转的性质得：AE＝AF，BE＝DF，∠BAE＝∠DAF，

在正方形ABCD中，∠BAD＝90°，

∵∠GAE＝45°，

∴∠BAE＋∠GAD＝45°，

∴∠DAF＋∠GAD＝45°，即∠GAF＝45°，

在△AGE和△AGF中，，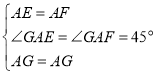

∴△AGE≌△AGF（SAS），

∴GE＝GF，

∵GF＝DG＋DF，BE＝DF，

∴GE＝DG＋BE；

（3）设DG＝x，则CG＝6－x，

∵BE＝DF＝2，

∴EC＝6－2＝4，GE＝GF＝x+2，

在Rt△CEG中，∵EC2+CG2＝GE2，

∴，

解得：x＝3，

即的长为3．