��Ŀ����
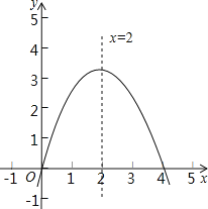
����Ŀ����ƽ��ֱ������ϵ�У���֪������y��![]() x2+kx+c��ͼ����C��0��1������x��2ʱ����������Сֵ��
x2+kx+c��ͼ����C��0��1������x��2ʱ����������Сֵ��
��1���������ߵĽ���ʽ��
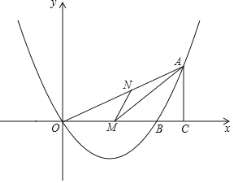
��2��ֱ��l��y�ᣬ��������Ϊ��0����1���������ߵĶԳ�����ֱ��l���ڵ�A����x������һ��B����AB��![]() ������ֱ��l�������ڵ�A��һ��Q��ʹ��Q�ڡ�ABC�����Բ�ϣ�
������ֱ��l�������ڵ�A��һ��Q��ʹ��Q�ڡ�ABC�����Բ�ϣ�
��3����P��a��b��Ϊ��������һ���㣬��MΪ����ϵ��һ���㣬����P��ֱ��l�ľ���ʼ�յ����߶�PM�ij�����M�����꣮
���𰸡���1��y��![]() x2��x+1�� ��2��Q��1����1������3��M��2��1��
x2��x+1�� ��2��Q��1����1������3��M��2��1��
��������
��1������֪���������߽���ʽΪy��![]() x2��x+1��
x2��x+1��
��2���������֪A��2����1������B��t��0������AB��![]() �����ԣ�t��2��2+1��2�����B��1��0����B��3��0������B��1��0��ʱ��A��B��C���㹲�ߣ���ȥ������B��3��0������֤����ABCΪֱ�������Σ�BCΪ���Բ��ֱ�������Բ��Բ��ΪBC���е㣨
�����ԣ�t��2��2+1��2�����B��1��0����B��3��0������B��1��0��ʱ��A��B��C���㹲�ߣ���ȥ������B��3��0������֤����ABCΪֱ�������Σ�BCΪ���Բ��ֱ�������Բ��Բ��ΪBC���е㣨![]() ��
��![]() �����뾶Ϊ
�����뾶Ϊ![]() ����Q��x����1�������У�x��
����Q��x����1��������x��![]() ��2+��
��2+��![]() +1��2����
+1��2����![]() ��2��������Q��1����1����
��2��������Q��1����1����
��3���趥��M��m��n����P��a��b��Ϊ��������һ���㣬����b��![]() a2��a+1����ΪP��ֱ��l�ľ������PM�����ԣ�m��a��2+��n��b��2����b+1��2���ɵ�
a2��a+1����ΪP��ֱ��l�ľ������PM�����ԣ�m��a��2+��n��b��2����b+1��2���ɵ�![]() +��2n��2m+2��a+��m2+n2��2n��3����0����aΪ����ֵ������ʽ����������
+��2n��2m+2��a+��m2+n2��2n��3����0����aΪ����ֵ������ʽ����������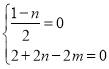 ������M�����꣮
������M�����꣮
�⣺��1����ͼ����C��0��1����
��c��1��
�ߵ�x��2ʱ����������Сֵ�����Գ���Ϊֱ��x��2��
��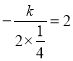 ����ã�k����1��
����ã�k����1��
�������߽���ʽΪy��![]() x2��x+1��
x2��x+1��
��2���������֪A��2����1������B��t��0����
��AB��![]() ��
��
�ࣨt��2��2+1��2��
��t��1��t��3��
��B��1��0����B��3��0����
��B��1��0��ʱ��A��B��C���㹲�ߣ���ȥ��
��B��3��0����
��AC��2![]() ��BC��
��BC��![]() ��
��
���BAC��90�㣬
���ABCΪֱ�������Σ�BCΪ���Բ��ֱ�������Բ��Բ��ΪBC���е㣨![]() ��
��![]() �����뾶Ϊ
�����뾶Ϊ![]() ��
��
��Q��x����1��������x��![]() ��2+��
��2+��![]() +1��2����
+1��2����![]() ��2��
��2��
��x��1��x��2����ȥ����
��Q��1����1����
��3���趥��M��m��n������P��a��b��Ϊ��������һ���㣬
��b��![]() a2��a+1��
a2��a+1��
��P��ֱ��l�ľ������PM��
�ࣨm��a��2+��n��b��2����b+1��2��
��![]() +��2n��2m+2��a+��m2+n2��2n��3����0��
+��2n��2m+2��a+��m2+n2��2n��3����0��
��aΪ����ֵ������ʽ��������
��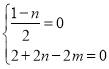 ��
��
��![]() ��
��
��ʱm2+n2��2n��3��0��
�ඨ��M��2��1����

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�