Question

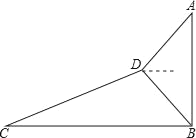
【题目】如图，在Rt△ABC中，∠ACB＝90°，∠A＝30°，BC＝4，以BC为直径的半圆O交斜边AB于点 D．

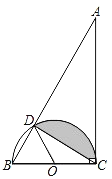
（1）证明：AD＝3BD；

（2）求弧BD的长度；

（3）求阴影部分的面积．

Answer 1

【答案】（1）见解析；（2）；（3）﹣

【解析】

（1）根据直角三角形的性质以及圆周角和圆心角的性质求出∠COD＝120°，结合圆的基本性质得出BC＝2BD，再根据直角三角形中30°角的性质得出AB＝2BC＝4BD，即可得出答案；

（2）根据弧长公式即可得出答案；

（3）根据割补法结合扇形的面积公式计算即可得出答案．

解：（1）∵在Rt△ABC中，∠ACB＝90°，∠A＝30°，

∴∠B＝60°，

∴∠COD＝120°，

∵BC＝4，BC为半圆O的直径，

∴∠CDB＝90°，

∴∠BCD＝30°，

∴BC＝2BD，

∵∠A＝30°，

∴AB＝2BC＝4BD，

∴AD＝3BD；

（2）由（1）得∠B＝60°，

∴OC＝OD＝OB＝2，

∴弧BC的长为；

（3）∵BC＝4，∠BCD＝30°，

∴CD＝BC＝，

图中阴影部分的面积＝S扇形COD﹣S△COD＝．