Question

【题目】如图，，是射线上一点，以为圆心，的长为半径作，使，是上一点，与相交于点，点与关于直线对称，连接．

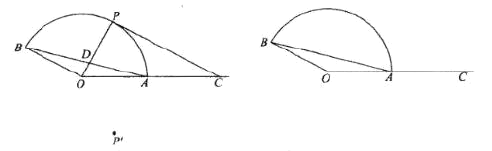
尝试： （1）点在所在的圆 （填“内”“上”或“外”）；

（2） ．

发现 ：（1）的最大值为 ；

（2）当，时，判断与所在圆的位置关系．

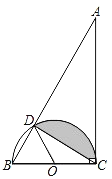
探究：当点与的距离最大时，求的长．（注：）

Answer 1

【答案】尝试：（1）上；（2）3；发现：（1）3；（2）相切，理由见解析；探究：

【解析】

尝试：（1）根据题意即可得到结论；
（2）如图1，延长AO交所在圆上的点E，连接BE，根据等腰三角形的性质得到∠BAO=∠ABO=14°，根据三角函数的定义即可得到结论；
发现：（1）在Rt△AOD中解直角三角形即可得到结论；
（2）根据弧长公式求得∠BOP=90°，根据切线的判定定理即可得到结论；
探究：作P′E⊥AB于点E，连接P′A，如图2，此时OE⊥AB，求得，根据勾股定理得到，，根据轴对称的性质即可得到AP=AP′=2．

尝试 （1）点P′在所在的圆上，
故答案为：上；
（2）如图1，延长AO交所在圆上的点E，
连接BE，
则∠ABE=90°，
∵∠AOB=152°，OB=OA，
∴∠BAO=∠ABO=14°，
∵OA=4，
∴AE=2OA=8，
∴AB=AEcos14°=8×=2，
故答案为：2；

发现 （1）当OP⊥AB时，PD有最大值，
在Rt△AOD中，∵OA=4，cos∠OAD= ，

∴AD=，
∴OD==1，
∴PD=4-1=3，
∴PD的最大值为3，
故答案为：3；

（2）相切．

理由如下：

当时，．

解得，即．

∵．

∴．

又，∴，

∵是半径，

∴与所在的圆相切．

探究 作于点．

∵点在所在的圆上，∴当过圆心时，最大．

连接，如图2．

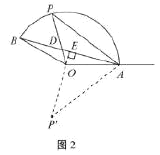
此时．

．

∵，

∴．

∵，∴．

∴．

又点，关于直线对称，

∴．