��Ŀ����
����Ŀ�������Ѿ�֪��һЩ����Ĺ����������������������еĹ�������3��4��5������������ż���еĹ�����6��8��10����ʵ�ϣ�������������������Ȼ�ǹ�������
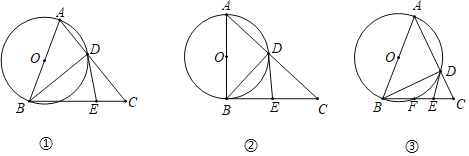
(1)��������һЩ���ɹ������Ĺ�ʽҲ����д������������ϴ����˹ѧ������Ĺ�ʽ��a��2n+1��b��2n2+2n��c��2n2+2n+1(nΪ������)��һ�鹴��������֤���������Ϲ�ʽ��a��b��c������һ�鹴������
(2)Ȼ���������ϵ�һ�θ����Ĺ�������ʽ���ռ����ҹ��Ŵ���������ѧ�����������������У������ᵽ����a��![]() (m2��n2)��b��mn��c��
(m2��n2)��b��mn��c��![]() (m2+n2)(m��nΪ��������m��nʱ��a��b��c����һ�鹴�����������������ۣ�����������⣺��֪ijֱ�������εı߳���������������������һ�߳�Ϊ37����n��5�����ֱ�������������ߵij���
(m2+n2)(m��nΪ��������m��nʱ��a��b��c����һ�鹴�����������������ۣ�����������⣺��֪ijֱ�������εı߳���������������������һ�߳�Ϊ37����n��5�����ֱ�������������ߵij���
���𰸡�(1)֤����������(2)��n��5ʱ��һ�߳�Ϊ37��ֱ�������������ߵij��ֱ�Ϊ12��35��
��������
��1����������ֻ��Ҫ֤��a2+b2��c2�����ɽ��
��2���������⽫n��5����õ�a��![]() (m2��52)��b��5m��c��
(m2��52)��b��5m��c��![]() (m2+25)���ٽ�ֱ�������ε�һ�߳�Ϊ37���ֱ�������������a��
(m2+25)���ٽ�ֱ�������ε�һ�߳�Ϊ37���ֱ�������������a��![]() (m2��52)��b��5m��c��
(m2��52)��b��5m��c��![]() (m2+25)�����ɽ��
(m2+25)�����ɽ��
(1)��a2+b2��(2n+1)2+(2n2+2n)2��4n2+4n+1+4n4+8n3+4n2��4n4+8n3+8n2+4n+1��
c2��(2n2+2n+1)2��4n4+8n3+8n2+4n+1��
��a2+b2��c2��
��n��������
��a��b��c��һ�鹴������
(2)�⣺��n��5
��a��![]() (m2��52)��b��5m��c��
(m2��52)��b��5m��c��![]() (m2+25)��
(m2+25)��
��ֱ�������ε�һ�߳�Ϊ37��
�������������ۣ�
�ٵ�a��37ʱ��![]() (m2��52)��37��
(m2��52)��37��
���m����3![]() (�������⣬��ȥ)
(�������⣬��ȥ)
�ڵ�y��37ʱ��5m��37��
���m��![]() (����������ȥ)��
(����������ȥ)��
�۵�z��37ʱ��37��![]() (m2+n2)��
(m2+n2)��
���m����7��
��m��n��0��m��n�ǻ��ʵ�������
��m��7��
��m��7����٢ڵã�x��12��y��35��
������������n��5ʱ��һ�߳�Ϊ37��ֱ�������������ߵij��ֱ�Ϊ12��35��

 �����Ծ���ĩ���100��ϵ�д�
�����Ծ���ĩ���100��ϵ�д� ˫��ͬ������ѵ��ϵ�д�
˫��ͬ������ѵ��ϵ�д� �Ƹ�С״Ԫͬ������������ϵ�д�
�Ƹ�С״Ԫͬ������������ϵ�д�����Ŀ��ijƷ���ֻ����۹�˾��Ӫ��Ա14�ˣ����۲�Ϊ�ƶ�Ӫ����Ա�������ֻ����ͳ������14��ij�µ����������£���λ��̨����
������ | 200 | 170 | 165 | 80 | 50 | 40 |
�� �� | 1 | 1 | 2 | 5 | 3 | 2 |
��1������14λӪ��Ա�������۸�Ʒ���ֻ���ƽ��������λ����������
��2�����۲�������ÿλӪ��Ա����������Ϊ100̨������Ϊ�Ƿ������Ϊʲô?