题目内容
【题目】如图,抛物线y=﹣x2+bx+c经过直线y=﹣x+5与坐标轴的交点B,C.已知D(0,3).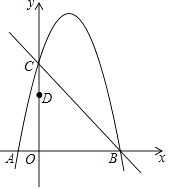
(1)求抛物线的解析式;
(2)M,N分别是BC,x轴上的动点,求△DMN周长最小时点M,N的坐标,并写出周长的最小值;
(3)连接BD,设M是平面上一点,将△BOD绕点M顺时针旋转90°后得到△B1O1D1 , 点B,O,D的对应点分别是B1 , O1 , D1 , 若△B1O1D1的两个顶点恰好落在抛物线上,请直接写出点O1的坐标.
【答案】
(1)解:由题意C(0,5),B(5,0),
把C(0,5),B(5,0)的坐标代入y=﹣x2+bx+c得到 ![]() ,
,
解得 ![]() ,
,
∴抛物线的解析式为y=﹣x2+4x+5.
(2)解:如图1中,作点D关于BC的对称点D′,点D关于x轴的对称点D″,连接D′D″交BC于M,交x轴于N,连接DM,DN.此时△DMN的周长最小.
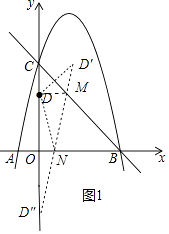
易知D′(2,5),D″(0,﹣3),
设直线D′D″的解析式为y=kx+b,则有 ![]() ,
,
解得 ![]() ,
,
∴y=4x﹣3,
∴N( ![]() ,0),
,0),
由 ![]() ,解得
,解得 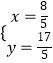 ,
,
∴M( ![]() ,
, ![]() ),
),
∴△DMN周长最小时点M( ![]() ,
, ![]() ),N(
),N( ![]() ,0),
,0),
△DMN的周长的最小值=D′D″= ![]() =2
=2 ![]() .
.
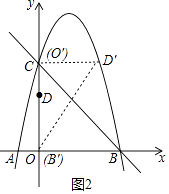
(3)解:①如图2中,当O′和D′在抛物线上时,易知点O′与点C重合,CD′=OD=3,此时O′(0,5).
②如图3中,点B′、D′在抛物线上时,设点B′(x,﹣x2+4x+5)的横坐标为x+1,则点D′的坐标为(x+3,﹣x2+4x+10).
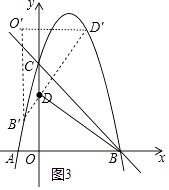
把D′坐标代入y=﹣x2+4x+5中,得到﹣x2+4x+10=﹣(x+3)2+4(x+3)+5,
解得x=﹣ ![]() ,
,
∴B′(﹣ ![]() ,
, ![]() ),
),
∴O′(﹣ ![]() ,
, ![]() ),
),
综上所述,满足条件的点O′的坐标为(0,5)或(﹣ ![]() ,
, ![]() ).
).
【解析】(1)求出B、C两点坐标,利用待定系数法即可解决问题;(2)如图1中,作点D关于BC的对称点D′,点D关于x轴的对称点D″,连接D′D″交BC于M,交x轴于N,连接DM,DN.此时△DMN的周长最小.求出D′、D″的坐标,直线D′D″的解析式即可解决问题;(3)分两种情形①如图2中,当O′和D′在抛物线上时,易知点O′与点C重合,CD′=OD=3,此时O′(0,5).②如图3中,点B′、D′在抛物线上时,设点B′(x,﹣x2+4x+5)的横坐标为x+1,则点D′的坐标为(x+3,﹣x2+4x+10).把D′的坐标代入抛物线的解析式,求出x即可解决问题;
【考点精析】掌握二次函数的性质是解答本题的根本,需要知道增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.

 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案