题目内容
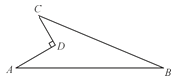
【题目】如图,AB为⊙O的直径,C为⊙O上一点,AD和过点C的切线互相垂直,垂足为D.求证:AC平分∠DAB.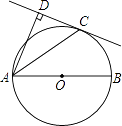
【答案】证明:连结OC,如图, 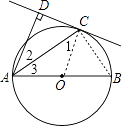
∵CD为⊙O的切线,
∴OC⊥AD,
∵AD⊥CD,
∴OC∥AD,
∴∠1=∠2,
∵OC=OA,
∴∠1=∠3,
∴∠2=∠3,
∴AC平分∠DAB.
【解析】连结OC,根据切线的性质得OC⊥AD,然后根据同一平面内垂直于同一直线的两条直线互相平行得出OC∥AD,故∠1=∠2,再根据等边对等角得出∠1=∠3,所以∠2=∠3。
【考点精析】掌握平行线的判定与性质和切线的性质定理是解答本题的根本,需要知道由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.

练习册系列答案
相关题目