题目内容
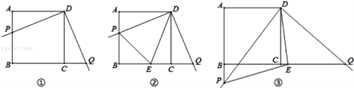
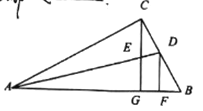
【题目】如图，在Rt△ABC中，∠ACB=90
，∠BAC的平分线交BC于D，过点C作CG⊥AB于G，交AD于E，过点D作DF⊥AB于F.下列结论①∠CED= 
；②
；③∠ADF= 
;④CE=DF.正确的是（ ）
A. ①②④ B. ②③④ C. ①③ D. ①②③④
【答案】A
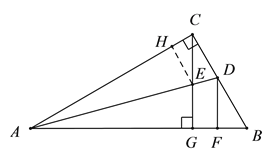
【解析】过点E作EH⊥AC，
∵AD平分∠CAB，CG⊥AB，∴EH=EG，
∴S△AEC：S△AEG= 
： 
=AC：AG，故②正确；
∵∠ACE+∠BCG=90°，∠B+∠BCG=90°，
∴∠ACE=∠B，
∵∠CED=∠CAE+∠ACE，∠CDE=∠B+∠DAB，∠CAE=∠BAD，
∴∠CED=∠CDE，故①正确；
∴CE=CD，
又AE平分∠CAB，DF⊥AB，AC⊥BC，
∴CD=DF，∴CE=DF，故④正确；
无法证明∠ADF=2∠FDB，
故选A．
练习册系列答案
寒假大串联黄山书社系列答案
相关题目
