Question

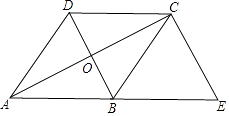
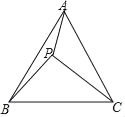
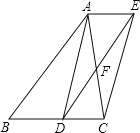
【题目】如图，已知点D是△ABC的边BC的中点，直线AE∥BC，过点D作直线DE∥AB，分别交AE、AC于点E、F。

（1）求证：四边形ADCE是平行四边形；

（2）如果四边形ADCE是矩形，△ABC应满足什么条件？并说明理由；

（3）如果四边形ADCE是菱形，直接写出△ABC应满足的条件是 。

Answer 1

【答案】（1）证明见解析；（2）如果四边形ADCE是矩形，则△ABC是等腰三角形，理由见解析；（3）AB⊥AC.

【解析】（1）证出四边形ABDE是平行四边形，得出AE=BD，由已知得出AE=CD，即可得出四边形ADCE是平行四边形．

（2）由矩形的性质得出∠ADB=90°，由线段垂直平分线的性质得出AB=AC即可．

（3）由菱形的性质得出AD=DC，根据BD=CD可知，B、A、C三点在以D为圆心的圆上，根据直径所对的圆周角是直角即可.

（1）证明：∵AE∥BC，DE∥AB，

∴四边形ABDE是平行四边形，

∴AE=BD，

∵点D是△ABC的边BC的中点，

∴BD=CD，

∴AE=CD，

∴四边形ADCE是平行四边形．

（2）解：如果四边形ADCE是矩形，△ABC是等腰三角形；理由如下：

∵四边形ADCE是矩形，

∴∠ADC=90°，

∴∠ADB=90°，即AD⊥BC，

∵点D是△ABC的边BC的中点，

∴AB=AC，

即△ABC是等腰三角形．

（3）△ABC应满足的条件是 AB⊥AC .