题目内容
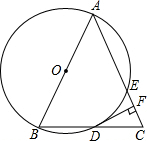
如图，在Rt△ABC中，∠C=90°，O是斜边AB上的一点，圆O过点A并与边BC相切于点D，与边AC相交于点E．
（1）求证：AD平分∠BAC；
（2）若圆O的半径为4，∠B=30°，求AC长．
（1）求证：AD平分∠BAC；
（2）若圆O的半径为4，∠B=30°，求AC长．
（1）连接DF，OD，则∠ADF=90°，
因为BC是⊙O的切线，
所以∠CDA=∠DFA，△ACD≌△ADF，∠CAD=∠DAB．
即AD是∠CAB的角平分线．
（2）∵∠B=30°，
∴∠CAB=60°；由（1）可知AD是∠CAB的平分线，
故∠CAD=∠DAB=30°；在Rt△ADF中，∠DAB=30°，AF=2×4=8．
故AD=AF•cos30°=8×
=4
．
同理，AC=AD•cos30°=4
×
=6．故AD=4
．AC=6．
因为BC是⊙O的切线，
所以∠CDA=∠DFA，△ACD≌△ADF，∠CAD=∠DAB．
即AD是∠CAB的角平分线．
（2）∵∠B=30°，
∴∠CAB=60°；由（1）可知AD是∠CAB的平分线，
故∠CAD=∠DAB=30°；在Rt△ADF中，∠DAB=30°，AF=2×4=8．
故AD=AF•cos30°=8×
| ||
| 2 |
| 3 |
同理，AC=AD•cos30°=4
| 3 |
| ||
| 2 |
| 3 |
练习册系列答案
阅读快车系列答案
相关题目
