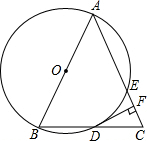
题目内容
如图所示,已知△ABC中,AB=AC,以AB为直径作⊙O交BC于D,交AC于E,过D作DF⊥AC于F.
(1)求证:DF是⊙O的切线;
(2)连接DE,若AB=AC=13,BC=10,求△CDE的面积.
(1)求证:DF是⊙O的切线;
(2)连接DE,若AB=AC=13,BC=10,求△CDE的面积.

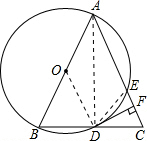
(1)连接OD,AD,
∵AB是⊙O的直径,
∴AD⊥BC,
∵AB=AC,
∴DB=DC,
∵OA=OB,
∴OD是△ABC的中位线,
即:OD∥AC,
∵DF⊥AC,
∴DF⊥OD.
∴DF是⊙O的切线.
(2)∵ABDE是⊙O的内接四边形,
∴∠DEC=∠B,又∠C为公共角,
∴△CDE∽△CAB,
∵AB=13,BC=10,由(1)得AD⊥BC,
∴CD=5,
∴AD=12.
S△ABC=
BC•AD=
×10×12=60.
∵△CDE∽△CAB,
∴
=
=
.
∴S△CDE:S△CAB=25:169.
∴S△CDE=60×
=
.
∵AB是⊙O的直径,
∴AD⊥BC,
∵AB=AC,
∴DB=DC,
∵OA=OB,
∴OD是△ABC的中位线,
即:OD∥AC,
∵DF⊥AC,
∴DF⊥OD.
∴DF是⊙O的切线.
(2)∵ABDE是⊙O的内接四边形,
∴∠DEC=∠B,又∠C为公共角,
∴△CDE∽△CAB,
∵AB=13,BC=10,由(1)得AD⊥BC,
∴CD=5,
∴AD=12.
S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∵△CDE∽△CAB,
∴
| DE |
| AB |
| CD |
| CA |
| 5 |
| 13 |
∴S△CDE:S△CAB=25:169.
∴S△CDE=60×
| 25 |
| 169 |
| 1500 |
| 169 |


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目







