Question

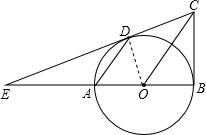
如图，已知AB是⊙O的直径，BC⊥AB，连结OC，弦AD∥OC，直线CD交BA的延长线于点E．
（1）求证：直线CD是⊙O的切线；
（2）若DE=2BC，求AD：OC的值．

Answer 1

（1）证明：连结DO．
∵AD∥OC，
∴∠DAO=∠COB，∠ADO=∠COD．…（1分）
又∵OA=OD，
∴∠DAO=∠ADO，
∴∠COD=∠COB．…（2分）
在△COD和△COB中，

CO=CO ∠COD=∠COB OD=OB

，
∴△COD≌△COB（SAS）…（3分）
∴∠CDO=∠CBO=90°．
又∵点D在⊙O上，
∴CD是⊙O的切线．…（4分）

（2）∵△COD≌△COB．
∴CD=CB．…（5分）
∵DE=2BC，
∴ED=2CD．…（6分）
∵AD∥OC，
∴△EDA∽△ECO．…（7分）
∴

AD

OC

=

DE

CE

=

2

3

．…（8分）