题目内容
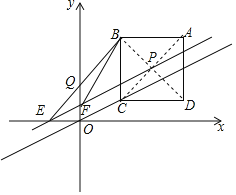
【题目】如图，在平面直角坐标系中，边长为3的正方形ABCD在第一象限内，AB∥x轴，点A的坐标为（5，4）经过点O、点C作直线l，将直线l沿y轴上下平移．
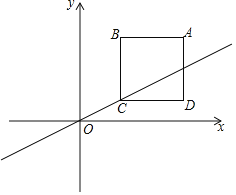
（1）当直线l与正方形ABCD只有一个公共点时，求直线l的解析式；
（2）当直线l在平移过程中恰好平分正方形ABCD的面积时，直线l分别与x轴、y轴相交于点E、点F，连接BE、BF，求△BEF的面积．
【答案】（1）y＝
x+3或y＝x﹣
；（2）
【解析】
（1）根据题意求得正方形各顶点的坐标，然后根据待定系数法求得直线l的解析式，直线平移，斜率不变，设平移后的直线方程为y＝
x+b；把点B和D的坐标代入进行解答即可；
（2）根据正方形是中心对称图形，当直线l经过对角线的交点时，恰好平分正方形ABCD的面积，求得交点坐标，代入y＝x+b，根据待定系数法即可求得直线l的解析式，然后求得E、F的坐标，根据待定系数法求得直线BE的解析式，得到与y轴的交点Q的坐标，根据三角形面积公式即可求得．
（1）∵长为3的正方形ABCD中，点A的坐标为（5，4），
∴B（2，4），C（2，1），D（5，1），
设直线l的解析式为y＝kx，
把C（2，1）代入得，1＝2k，解得k＝，
∴直线l为：y＝
，
设平移后的直线方程为y＝x+b，
把点B的坐标代入，得:4＝×2+b，
解得 b＝3，
把点D的坐标代入，得:1＝×5+b，
解得: b＝﹣
，
则平移后的直线l解析式为：y＝x+3或y＝x﹣；
（2）设AC和BD的交点为P，
∴P点的坐标为（
，
），
把P点的坐标代入y＝x+b得，＝
+b，
解得b＝
，
∴此时直线l的解析式为y＝x+，如图，
∴E（﹣，0），F（0，），
设直线BE的解析式为：y＝mx+n，
则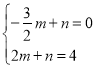
，解得：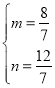
，
∴直线BE的解析式为：y＝
x+
，
∴Q（0，），
∴QF＝﹣＝
，
∴△BEF的面积＝
＝．
