题目内容
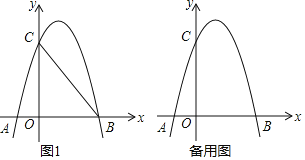
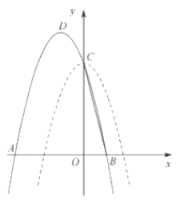
【题目】已知函数y=ax2+bx+c(a≠0,a、b、c为常数)的图像经过点A(-1,0)、B(0,2).
(1)b= (用含有a的代数式表示),c= ;
(2)点O是坐标原点,点C是该函数图像的顶点,若△AOC的面积为1,则a= ;
(3)若x>1时,y<5.结合图像,直接写出a的取值范围.
【答案】(1)a+2;2;(2)-2或![]() ;(3)
;(3)![]()
【解析】
(1)将点B的坐标代入解析式,求得c的值;将点A代入解析式,从而求得b;;(2)由题意可得AO=1,设C点坐标为(x,y),然后利用三角形的面积求出点C的纵坐标,然后代入顶点坐标公式求得a的值;(3)结合图像,若x>1时,y<5,则顶点纵坐标大于等于5,根据顶点纵坐标公式列不等式求解即可.
解:(1)将B(0,2)代入解析式得:c=2
将A(-1,0)代入解析式得: a×(-1)2+b×(-1)+c=0
∴a-b+2=0
∴b=a+2
故答案为:a+2;2
(2)由题意可知:AO=1
设C点坐标为(x,y)
则![]()
解得:![]()
当y=2时,![]()
由(1)可知,b=a+2;c=2
∴![]()
解得:a=-2
当y=-2时,![]()
由(1)可知,b=a+2;c=2
∴![]()
解得:![]()
∴a的值为-2或![]()
(3)若x>1时,y<5,又因为图像过点A(-1,0)、B(0,2)
∴图像开口向下,即a<0
则该图像顶点纵坐标大于等于5
∴![]()
即![]()
解得:![]() 或
或![]() (舍去)
(舍去)
∴a的取值范围为![]()

【题目】学校为了解九年级学生对“八礼四仪”的掌握情况,对该年级的500名同学进行问卷测试,并随机抽取了10名同学的问卷,统计成绩如下:
得分 | 10 | 9 | 8 | 7 | 6 |
人数 | 3 | 3 | 2 | 1 | 1 |
(1)计算这10名同学这次测试的平均得分;
(2)如果得分不少于9分的定义为“优秀”,估计这 500名学生对“八礼四仪”掌握情况优秀的人数;
(3)小明所在班级共有40人,他们全部参加了这次测试,平均分为7.8分.小明的测试成绩是8分,小明说,我的测试成绩在班级中等偏上,你同意他的观点吗?为什么?