题目内容
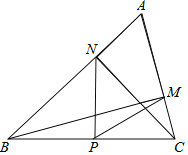
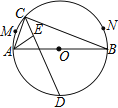
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() 、
、![]() 是弧
是弧![]() (异于
(异于![]() 、
、![]() )上两点,
)上两点,![]() 是弧
是弧![]() 上一动点,
上一动点,![]() 的角平分线交
的角平分线交![]() 于点
于点![]() ,
,![]() 的平分线交
的平分线交![]() 于点
于点![]() .当点
.当点![]() 从点
从点![]() 运动到点
运动到点![]() 时,则
时,则![]() 、
、![]() 两点的运动路径长的比是( )
两点的运动路径长的比是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
连接BE,由题意可得点E是△ABC的内心,由此可得∠AEB=135°,为定值,确定出点E的运动轨迹是是弓形AB上的圆弧,此圆弧所在圆的圆心在AB的中垂线上,根据题意过圆心O作直径CD,则CD⊥AB,在CD的延长线上,作DF=DA,则可判定A、E、B、F四点共圆,继而得出DE=DA=DF,点D为弓形AB所在圆的圆心,设⊙O的半径为R,求出点C的运动路径长为![]() ,DA=
,DA=![]() R,进而求出点E的运动路径为弧AEB,弧长为
R,进而求出点E的运动路径为弧AEB,弧长为![]() ,即可求得答案.
,即可求得答案.
连结BE,
∵点E是∠ACB与∠CAB的交点,
∴点E是△ABC的内心,
∴BE平分∠ABC,
∵AB为直径,
∴∠ACB=90°,
∴∠AEB=180°-![]() (∠CAB+∠CBA)=135°,为定值,
(∠CAB+∠CBA)=135°,为定值,![]() ,
,
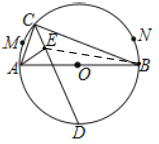
∴点E的轨迹是弓形AB上的圆弧,
∴此圆弧的圆心一定在弦AB的中垂线上,
∵![]() ,
,
∴AD=BD,
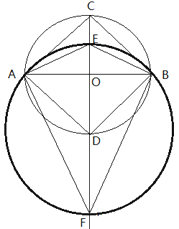
如下图,过圆心O作直径CD,则CD⊥AB,
∠BDO=∠ADO=45°,
在CD的延长线上,作DF=DA,
则∠AFB=45°,
即∠AFB+∠AEB=180°,
∴A、E、B、F四点共圆,
∴∠DAE=∠DEA=67.5°,
∴DE=DA=DF,
∴点D为弓形AB所在圆的圆心,
设⊙O的半径为R,
则点C的运动路径长为:![]() ,
,
DA=![]() R,
R,
点E的运动路径为弧AEB,弧长为:![]() ,
,
C、E两点的运动路径长比为: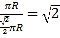 ,
,
故选A.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目