Question

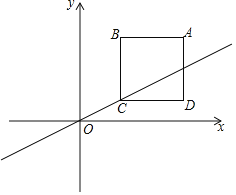
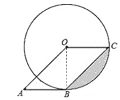
【题目】如图，四边形OABC为平行四边形，B、C在⊙O上，A在⊙O外，sin∠OCB=．

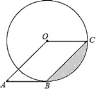
（1）求证：AB与⊙O相切；

（2）若BC=10cm，求图中阴影部分的面积．

Answer 1

【答案】（1）见解析（2）.

【解析】

连接OB，由sin∠OCB=求出∠OCB=45，再根据OB=OC及三角形的内角和求出

∠BOC=90，再由四边形OABC为平行四边形，得出∠ABO=90即OB⊥AB，由此切线得到证明；

（2）先求出半径，再由-S△BOC即可求出阴影部分的面积.

连接OB，

∵sin∠OCB=，

∴∠OCB=45，

∵OB=OC，

∴∠OBC=∠OCB=45，

∴∠BOC=90，

∵四边形OABC为平行四边形，

∴OC∥AB，

∴∠ABO=90,即OB⊥AB，

∴AB与⊙O相切；

（2）在Rt△OBC中，BC=10，sin∠OCB=，

∴，

∴-S△BOC=.