��Ŀ����
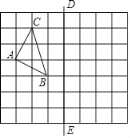
����Ŀ����ͼ��������BA��BC��AD��CDΧ�ɵ�����ABCD�У���ABC=60�㣬AB=6 ![]() ��O������BD��һ�㣬��O��BA��BC�����У���BO���ӳ��߽��ڵ�M����M��EF��BD���߶�BA��������AD���ڵ�E�����߶�BC��������CD���ڵ�F����EFΪ��������EFGH����G��H�ֱ���Χ�����ε��������������ϣ�
��O������BD��һ�㣬��O��BA��BC�����У���BO���ӳ��߽��ڵ�M����M��EF��BD���߶�BA��������AD���ڵ�E�����߶�BC��������CD���ڵ�F����EFΪ��������EFGH����G��H�ֱ���Χ�����ε��������������ϣ� 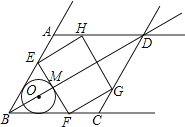
��1����֤��BO=2OM��
��2����EF��HE��������EFGH�����Ϊ24 ![]() ʱ�����O�İ뾶��
ʱ�����O�İ뾶��
��3����HE��HG���O����ʱ�������������������BO�ij���
���𰸡�
��1��
֤������ͼ1��ʾ�����O��AB�ڵ�P������OP�����OPB=90�㣮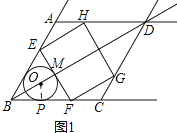
���ı���ABCDΪ���Σ�
���ABD= ![]() ��ABC=30�㣮
��ABC=30�㣮
��OB=2OP��
��OP=OM��
��BO=2OP=2OM��
��2��
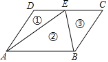
�⣺��ͼ2��ʾ����GH��BD�ڵ�N������AC����BD�ڵ�Q��
���ı���ABCD�����Σ�
��AC��BD��
��BD=2BQ=2ABcos��ABQ= ![]() AB=18��
AB=18��
���O�İ뾶Ϊr����OB=2r��MB=3r��
��EF��HE��
���E��F��G��H�������εı��ϣ�
����ͼ2��ʾ������E��AB��ʱ��
��Rt��BEM��EM=BMtan��EBM= ![]() r��
r��
�ɶԳ��Եã�EF=2EM=2 ![]() r��ND=BM=3r��
r��ND=BM=3r��
��MN=18��6r��
��S����EFGH=EFMN=2 ![]() r��18��6r��=24
r��18��6r��=24 ![]() ��
��
��ã�r1=1��r2=2��
��r=1ʱ��EF��HE��
��r=1ʱ������������
��r=2ʱ��EF��HE��
���O�İ뾶Ϊ2��
��BM=3r=6��
��ͼ3��ʾ��
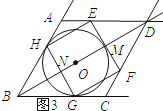
����E��AD����ʱ��BM=3r����MD=18��3r��
�ɶԳ��Կ�֪��NB=MD=6��
��MB=3r=18��6=12��
��ã�r=4��
������������O�İ뾶Ϊ2��4��
��3��
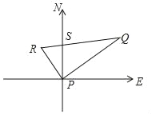
�⣺����GH��BD�ڵ�N����O�İ뾶Ϊr����BO=2r��
����E�ڱ�BA��ʱ����Ȼ������HE��HG���O���У�
����ͼ4��ʾ����E��AD��ʱ��
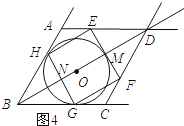
��HE���O����
��ME=r��DM= ![]() r��
r��
��3r+ ![]() r=18��
r=18��
��ã�r=9��3 ![]() ��
��
��OB=18��6 ![]() ��
��
����ͼ5��ʾ��
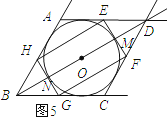
��ͼ�εĶԳ��Եã�ON=OM��BN=DM��
��OB= ![]() BD=9��
BD=9��
����ͼ6��ʾ��
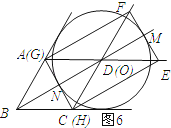
��HG���O����ʱ��MN=2r��
��BN+MN=BM=3r��
��BN=r��
��DM= ![]() FM=
FM= ![]() GN=BN=r��
GN=BN=r��
��D��O�غϣ�
��BO=BD=18��
����ͼ7��ʾ��
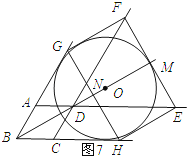
��HE���O����
��EM=r��DM= ![]() r��
r��
��3r�� ![]() r=18��
r=18��
��r=9+3 ![]() ��
��
��OB=2r=18+6 ![]() ��
��
������������HE��GH���O����ʱ��OB�ij�Ϊ18��6 ![]() ��9��18��18+6
��9��18��18+6 ![]() ��
��
����������1�����O��AB�ڵ�P������OP�������ߵ����ʿ�֪��OPB=90�㣮�������ε�������á�OBP�Ķ�����Ȼ�����ݺ�30��ֱ�������ε�����֤�����ɣ�
����������2����GH��BD�ڵ�N������AC����BD�ڵ�Q������������������Ǻ���ֵ���BD�ij������O�İ뾶Ϊr����OB=2r��MB=3r������E��AB��ʱ����Rt��BEM�У���������������Ǻ���ֵ�ɵõ�EM�ij����ú�r��ʽ�ӱ�ʾ������ͼ�εĶԳ��Կɵõ�EF��ND��BM�ij����ú�r��ʽ�ӱ�ʾ���Ӷ��õ�MN=18��6r�����������ݾ��ε�����з�����⼴�ɣ�����E��AD����ʱ��BM=3r����MD=18��3r�������MB=3r=12�з�����⼴�ɣ�
����������3���ȸ������⻭�����������ͼ�Σ�
������������ͼ4��ʾ����E��AD��ʱ�������DM= ![]() r��BM=3r��Ȼ������BM+MD=18���з�����⼴�ɣ�
r��BM=3r��Ȼ������BM+MD=18���з�����⼴�ɣ�
������������ͼ5��ʾ������ͼ�εĶԳ��Կ�֪�õ�OB= ![]() BD��
BD��
������������ͼ6��ʾ����֤��D��O�غϣ��Ӷ������OB�ij���
������������ͼ7��ʾ�������DM= ![]() r��OMB=3r����BM��DM=DB�з�����⼴�ɣ�������Ҫ��������ı��ε��ۺ�Ӧ�ã��������ҪӦ�������ε����ʡ����ߵ����ʡ�����������Ǻ���ֵ��Ӧ�á����ε������ʽ���������⻭�����������ͼ���ǽ���Ĺؼ���
r��OMB=3r����BM��DM=DB�з�����⼴�ɣ�������Ҫ��������ı��ε��ۺ�Ӧ�ã��������ҪӦ�������ε����ʡ����ߵ����ʡ�����������Ǻ���ֵ��Ӧ�á����ε������ʽ���������⻭�����������ͼ���ǽ���Ĺؼ���