题目内容
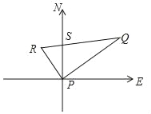
【题目】如图,某港口P位于东西方向的海岸线上,A、B两艘轮船同时从港口P出发,各自沿一固定方向航行,A轮船每小时航行12海里,B轮船每小时航行16海里.它们离开港口一个半小时后分别位于点R、Q处,且相距30海里.已知B轮船沿北偏东60°方向航行.
(1)A轮船沿哪个方向航行?请说明理由;
(2)请求出此时A轮船到海岸线的距离.
【答案】(1)A轮船沿北偏东30°方向航行;(2)此时A轮船到海岸线的距离为9![]() 海里.
海里.
【解析】
(1)根据题意得出RP=18海里,PQ=24海里,QR=30海里,利用勾股定理逆定理以及方向角得出答案;
(2)过点R作RM⊥PE于点M,然后利用sin60°=![]() ,得出答案.
,得出答案.
解:(1)由题意可得:RP=18海里,PQ=24海里,QR=30海里,
∵182+242=302,
∴△RPQ是直角三角形,
∴∠RPQ=90°,
∵B轮船沿北偏东60°方向航行,
∴∠RPS=30°,
∴A轮船沿北偏东30°方向航行;
(2)过点R作RM⊥PE于点M,则∠RPM=60°,
则sin60°=![]() ,
,
解得:RM=9![]() .
.
答:此时A轮船到海岸线的距离为9![]() 海里.
海里.

练习册系列答案
相关题目
【题目】世界上大部分国家都使用摄氏温度(℃),但美国,英国等国家的天气预报都使用华氏温度(℉),两种计量之间有如下对应:
摄氏温度(℃) | … | 0 | 10 | … |
华氏温度(℉) | … | 32 | 50 | … |
已知华氏温度y(℉)是摄氏温度x(℃)的一次函数.
求该一次函数的解析式;
当华氏温度14℉时,求其所对应的摄氏温度.