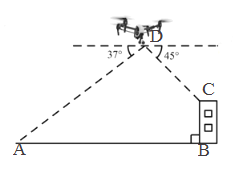
题目内容
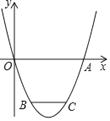
【题目】如图，抛物线y=ax2+3x+c经过A（﹣1，0），B（4，0）两点，与y轴交于点C．
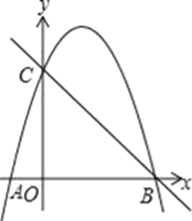
（1）求抛物线的解析式；
（2）若点P在第一象限的抛物线上，且点P的横坐标为t，过点P向x轴作垂线交直线BC于点Q，设线段PQ的长为m，求m与t之间的函数关系式，并求出m的最大值；
（3）在（2）的条件下，抛物线上点D（不与C重合）的纵坐标为m的最大值，在x轴上找一点E，使点B、C、D、E为顶点的四边形是平行四边形，请直接写出E点坐标．
【答案】（1）
；（2）
，当
时，
的最大值为4；（3）
或
【解析】
（1）将点
、
的坐标代入抛物线的解析式得到关于
、
的方程组，从而可求得、的值；
（2）先求得点
的坐标，然后依据待定系数法求得直线
的解析式，由直线可抛物线的解析式可知
，
，从而可求得
与
的关系式，最后依据配方法可求得的最大值；
（3）将
代入抛物线的解析式求得点
的坐标，依据一组对边平行且相等的四边形是平行四边形可得到
时，、、、
为顶点的四边形是平行四边形，从而可求得点的坐标．
解（1）
抛物线
经过
，
两点，
．
解得：
，
．
抛物线的解析式为．
（2）将
代入抛物线的解析式得：，
．
设直线的解析式为
．
将，
代入得：
，解得：
，
直线的解析式为：
．
过点
作
的垂线
交于点Q，如图所示：
点的横坐标为，
，．
．
．
当时，的最大值为4．
（3）将代入抛物线的解析式得：
．
解得：
，
．
点与点不重合，
点的坐标为
．
又
轴，
．
当时，、、、为顶点的四边形是平行四边形．
点
或
．
开心快乐假期作业暑假作业西安出版社系列答案
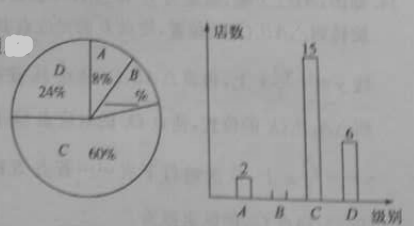
名题训练系列答案
【题目】全民健身运动已成为一种时尚，为了了解我市居民健身运动的情况，某健身馆的工作人员开展了一项问卷调查，问卷包括五个项目：A：健身房运动；B：跳广场舞；C：参加暴走团；D：散布；E：不运动．
以下是根据调查结果绘制的统计图表的一部分．
运动形式 | A | B | C | D | E |
人数 | 12 | 30 | m | 54 | 9 |
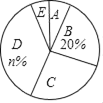
请你根据以上信息，回答下列问题：
（1）接受问卷调查的共有 人，图表中的m= ，n= ；
（2）统计图中，A类所对应的扇形圆心角的度数为 ；
（3）根据调查结果，我市市民最喜爱的运动方式是 ，不运动的市民所占的百分比是 ；
（4）郑州市碧沙岗公园是附近市民喜爱的运动场所之一，每晚都有“暴走团”活动，若最邻近的某社区约有1500人，那么估计一下该社区参加碧沙岗“暴走团”的大约有多少人？
