题目内容
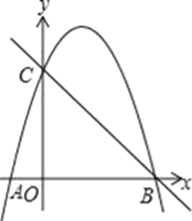
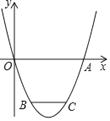
【题目】已知开口向上的抛物线![]() 交
交![]() 轴于点
轴于点![]() ,
,![]() ,函数值
,函数值![]() 的最小值是
的最小值是![]() .
.
(1)求抛物线的解析式.
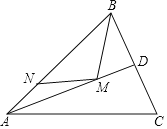
(2)点![]() 为抛物线上的点,并在对称轴的左侧.作
为抛物线上的点,并在对称轴的左侧.作![]() 轴交抛物线于点
轴交抛物线于点![]() ,连结
,连结![]() ,
,![]() ,且
,且![]() .
.
①求![]() 的值.
的值.
②若点![]() 在线段
在线段![]() 上,以点
上,以点![]() 为圆心,
为圆心,![]() 为半径画圆.当
为半径画圆.当![]() 和
和![]() 的一边相切时,求点
的一边相切时,求点![]() 的横坐标.
的横坐标.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②
;②![]() 或
或![]() .
.
【解析】
(1)将抛物线![]() 变形为
变形为![]() ,由函数值
,由函数值![]() 的最小值是
的最小值是![]() ,得
,得![]() ,求得
,求得![]() ,即可得到抛物线的解析式;
,即可得到抛物线的解析式;
(2)①连接![]() ,过点B作BD⊥OA于点D,由抛物线的解析式,可求得抛物线的对称轴、B的横坐标、C的横坐标,继而可求得B的坐标和C的坐标,可求得
,过点B作BD⊥OA于点D,由抛物线的解析式,可求得抛物线的对称轴、B的横坐标、C的横坐标,继而可求得B的坐标和C的坐标,可求得![]() 、
、![]() ;然后根据平行线的性质,可得
;然后根据平行线的性质,可得![]() ,继而可得
,继而可得![]() ,则可得到
,则可得到![]() 的值;
的值;
②由题意和图象得,![]() 与
与![]() 不相切,所以需要分
不相切,所以需要分![]() 与
与![]() 相切、
相切、![]() 与
与![]() 相切两种情况进行分类讨论.当
相切两种情况进行分类讨论.当![]() 与
与![]() 相切时,
相切时,![]() ⊥
⊥![]() ,由C的横坐标为
,由C的横坐标为![]() ,得
,得![]() 的横坐标也为
的横坐标也为![]() ;当
;当![]() 与
与![]() 相切时,
相切时, ![]() ⊥
⊥![]() ,过
,过![]() 、
、![]() 分别作直线
分别作直线![]() 的垂线
的垂线![]() 、
、![]() ,交点分别为
,交点分别为![]() 、
、![]() ,过
,过![]() 作
作![]() ⊥
⊥![]() 于
于![]() ,根据
,根据![]() ,设
,设![]() ,
,![]() ,继而得
,继而得![]() ,又
,又![]() ,
,![]() ,然后根据
,然后根据![]() ,有
,有![]() ,从而求得b,得到
,从而求得b,得到![]() ,即可得出
,即可得出![]() 的横坐标.
的横坐标.
(1)![]() ,
,
∵函数值![]() 的最小值是
的最小值是![]() ,
,
∴![]() ,解得:
,解得:![]() ,
,
∴抛物线的解析式为:![]() ;
;
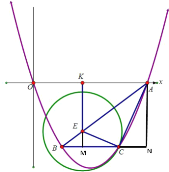
(2)①如图,连接![]() ,过点B作BD⊥OA于点D,
,过点B作BD⊥OA于点D,
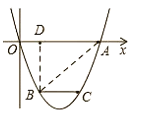
∵抛物线的解析式为:![]() ,
,
∴A(6,0),OA=6,抛物线的对称轴为直线x=3,
∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,![]() ,
,
即点B的横坐标为![]() ,点C的横坐标为
,点C的横坐标为![]() ,
,
将![]() ,
,![]() 分别代入抛物线
分别代入抛物线![]() ,得
,得![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() 轴,∴
轴,∴![]() ,
,
∴ ,
,
即![]() 的值为
的值为![]() ;
;
②由题意和图象可得,![]() 与
与![]() 不相切,所以需要分
不相切,所以需要分![]() 与
与![]() 相切、
相切、![]() 与
与![]() 相切两种情况:
相切两种情况:
当![]() 与
与![]() 相切时,由
相切时,由![]() 以点
以点![]() 为圆心、
为圆心、![]() 为半径,可得切点为点
为半径,可得切点为点![]() ,即
,即![]() ⊥
⊥![]() ,
,
如图,延长![]() 交
交![]() 于点
于点![]() ,则
,则![]() ⊥
⊥![]() ,
,
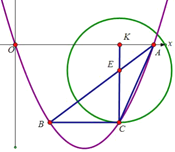
∵![]() ⊥
⊥![]() ,C的横坐标为
,C的横坐标为![]() ,
,
∴![]() 的横坐标为
的横坐标为![]() ;
;
当![]() 与
与![]() 相切时,则切点为点
相切时,则切点为点![]() ,即
,即![]() ⊥
⊥![]() ,
,
如图,分别过![]() 、
、![]() 分别作直线
分别作直线![]() 的垂线
的垂线![]() 、
、![]() ,交点分别为
,交点分别为![]() 、
、![]() ,过E作
,过E作![]() ⊥
⊥![]() 于
于![]() ,
,
由(2)①得![]() ,则设
,则设![]() ,
,![]() ,
,
∴![]() ,
,
由(2)①得OA=6,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
可证![]() ,则有
,则有![]() ,即
,即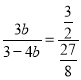 ,解得
,解得![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() 的横坐标为
的横坐标为![]() ,
,
综上可得,![]() 的横坐标为
的横坐标为![]() 或
或![]() .
.

 名校课堂系列答案
名校课堂系列答案