题目内容
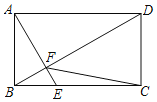
【题目】如图,在矩形ABCD中,点E是BC边上的一点,且AE⊥BD,垂足为点F,∠DAE=2∠BAE.
(1)求证:BF:DF=1:3;
(2)若四边形EFDC的面积为11,求△CEF的面积.
【答案】(1)详见解析;(2)2.
【解析】
(1)根据已知条件得到∠DAE=60°,∠BAE=30°,又AE⊥BD,得到![]() ,
, ![]() ,于是得到结论;
,于是得到结论;
(2)根据已知条件得到△BEF∽△BDC,求得∠ABF=60°,得到∠FBE=30°,求得![]() ,
,
![]() ,由于BD=4BF,得到
,由于BD=4BF,得到![]() ,根据三角形的面积公式即可得到结论.
,根据三角形的面积公式即可得到结论.
(1)证明:∵四边形ABCD为矩形,∠DAE=2∠BAE,
∴∠DAE=60°,∠BAE=30°,
又∵AE⊥BD,
∴![]() ,
,![]() ,
,
∴BF:DF=1:3;
(2)解:∵∠FBE=∠CBD,∠BFE=∠DCB,
∴△BEF∽△BDC,
∵∠BAE=30°,
∴∠ABF=60°,
∴∠FBE=30°,
∴![]() ,
,
∴![]() ,
,
∵BD=4BF,
∴![]() ,
,
∴![]()
![]() ,
,
∵S四边形EFDC=11,
∴S△BEF=1,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴S△CEF=1×2=2.

练习册系列答案
相关题目