题目内容
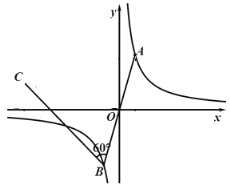
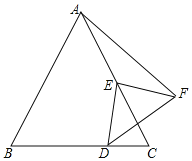
【题目】如图:△ABC是等边三角形,AB=12,E是AC中点,D是直线BC上一动点,线段ED绕点E逆时针旋转90°,得线段EF,当点D运动时,则线段AF的最小值为_____.
【答案】3+3![]()
【解析】
连接BE,延长EC到N,使EN=BE,连接FN,过点A作AG⊥BC于G,过点A作AH⊥FN于H,由等边三角形的性质可得AC=AB=12,AE=EC=6,BE⊥AC,∠GAC=∠EBC=30°,BE=6![]() =EN,由旋转的性质可得DE=EF,∠DEF=90°,由“SAS“可证△BED≌△NEF,可得∠EBC=∠ENF=30°,可得点F在过点N且平行于AG的直线上,当AF⊥FN时,AF的值最小,由直角三角形的性质可求线段AF的最小值.
=EN,由旋转的性质可得DE=EF,∠DEF=90°,由“SAS“可证△BED≌△NEF,可得∠EBC=∠ENF=30°,可得点F在过点N且平行于AG的直线上,当AF⊥FN时,AF的值最小,由直角三角形的性质可求线段AF的最小值.
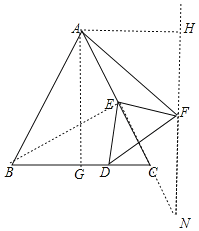
解:如图,连接BE,延长EC到N,使EN=BE,连接FN,过点A作AG⊥BC于G,过点A作AH⊥FN于H,
∵△ABC是等边三角形,AB=12,E是AC中点,AG⊥BC,
∴AC=AB=12,AE=EC=6,BE⊥AC,∠GAC=∠EBC=30°,BE=![]() =6
=6![]() =EN,
=EN,
∵线段ED绕点E逆时针旋转90°,
∴DE=EF,∠DEF=90°,
∵∠BEC=∠DEF=90°,
∴∠BED=∠FEN,且DE=EF,BE=EN,
∴△BED≌△NEF(SAS),
∴∠EBC=∠ENF=30°,
∴∠GAC=∠ENF,
∴AG∥NF,
∴点F在过点N且平行于AG的直线上,
∴当AF⊥FN时,AF的值最小,
∵AH⊥FN,∠ENF=30°,
∴AH=![]() AN=
AN=![]() (6+6
(6+6![]() )=3+3
)=3+3![]() ,
,
∴线段AF的最小值为3+3![]() ,
,
故答案为:3+3![]() .
.

 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案【题目】某数学兴趣小组在探究函数y=|x2-4x+3|的图象和性质时,经历以下几个学习过程:
(1)列表(完成以下表格)
x | … | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
y1=x2-4x+3 | … | 15 | 8 | 0 | 0 | 3 | 15 | … | |||
y=|x2-4x+3| | … | 15 | 8 | 0 | 0 | 3 | 15 | … |
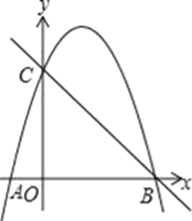
(2)描点并画出函数图象草图(在备用图1中描点并画图)

(3)根据图象完成以下问题
(ⅰ)观察图象
函数y=|x2-4x+3|的图象可由函数y1=x2-4x+3的图象如何变化得到?
答:______.
(ⅱ)数学小组探究发现直线y=8与函数y=|x2-4x+3|的图象交于点E、F,E(-1,8),F(5,8),则不等式|x2-4x+3|>8的解集是______;
(ⅲ)设函数y=|x2-4x+3|的图象与x轴交于A、B两点(B位于A的右侧),与y轴交于点C.
①求直线BC的解析式;
②探究应用:将直线BC沿y轴平移m个单位后与函数y=|x2-4x+3|的图象恰好有3个交点,求此时m的值.