Question

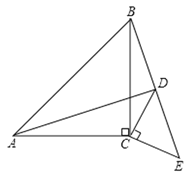
【题目】如图1，△ABC和△DEC均为等腰直角三角形，∠ACB=∠DCE=90°，点B，D，E在同一直线上，连接AD，BD．

（1）请探究AD与BD之间的位置关系并证明你的结论；

（2）若AC=BC=，DC=CE= ，求线段AD的长；

Answer 1

【答案】（1）AD⊥BD，证明见解析；（2）4．

【解析】

（1）由△ABC和△DEC均为等腰直角三角形，得∠ABC=∠DEC=∠CDE=45°，∠ACB=∠DCE=90°，进而证△ACD≌△BCE，即可得到结论；

（2）过点C作CF⊥AD于点F，根据等腰直角三角形的性质和勾股定理，即可求解．

（1）AD⊥BD，理由如下：

∵△ABC和△DEC均为等腰直角三角形，

∴AC=BC，CE=CD，∠ABC=∠DEC=∠CDE=45°，∠ACB=∠DCE=90°，∴∠ACD=∠BCE，

又∵AC=BC，CE=CD，

∴△ACD≌△BCE(SAS)

∴∠ADC=∠BEC=45°，

∴∠ADE=∠ADC+∠CDE=90°，

∴AD⊥BD；

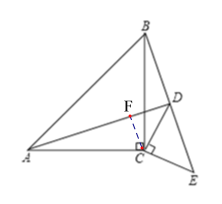
（2）过点C作CF⊥AD于点F，

∵∠ADC=45°，CF⊥AD，CD=，

∴DF=CF=1，

∵AC=BC=，

∴AF==3，

∴AD=AF+DF=4．