题目内容
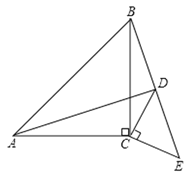
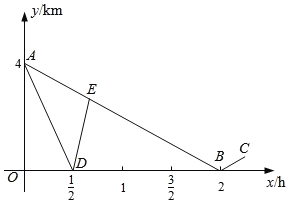
【题目】某校学生步行到郊外春游，一班的学生组成前队，速度为4km/h，二班的学生组成后队，速度为6km/h．前队出发1h后，后队才出发，同时，后队派一名联络员骑自行车在两队之间不间断的来回进行联络，他骑车的速度为akm/h．若不计队伍的长度，如图，折线A﹣B﹣C，A﹣D﹣E分别表示后队、联络员在行进过程中，离前队的路程y（km）与后队行进时间x（h）之间的部分函数图象．
（1）联络员骑车的速度a= ；
（2）求线段AD对应的函数表达式；
（3）求联络员折返后第一次与后队相遇时的时间．
【答案】（1）12；（2）y=﹣8x+4（0≤x
）；（3）联络员出发
h时第一次与后队相遇．
【解析】
(1)根据题目意思和函数图象中的数据可以求出a的值；
(2)根据函数图象中的数据可以得出A点和D点的左边，从而求得线段AD对应的函数表达式；
(3)根据题目意思和函数图象中的数据，设联络员折返后第一次与后队相遇的时间t时，列出方程即可求解．
解：(1)由图可得：
a=(4+4
)
12
故答案为：12；
(2)设线段AD对应的函数表达式为y=kx+b，
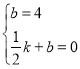，得
，
即线段AD对应的函数表达式为y=﹣8x+4(0≤x)；
(3)设联络员折返后第一次与后队相遇的时间t时，
(12+6)(t
)=4-(6﹣4)，
解得：t
，
答：联络员出发h时第一次与后队相遇．
阅读快车系列答案
【题目】如图，OABC的周长为14，∠AOC=60°，以O为原点，OC所在直线为x轴建立直角坐标系，函数y
（x＞0）的图象经过OABC的顶点A和BC的中点M，则k的值为（ ）
A.2
B.4C.6D.12
【题目】学校开展“书香校园”活动以来，受到同学们的广泛关注，学校为了解全校学生课外阅读的情况，随机调查了部分学生在一周内借阅图书的次数，并制成如图不完整的统计表．学生借阅图书的次数统计表
借阅图书的次数 | 0次 | 1次 | 2次 | 3次 | 4次及以上 |
人数 | 7 | 13 | a | 10 | 3 |
请你根据统计图表中的信息，解答下列问题：
______，
______．
该调查统计数据的中位数是______，众数是______．
请计算扇形统计图中“3次”所对应扇形的圆心角的度数；
若该校共有2000名学生，根据调查结果，估计该校学生在一周内借阅图书“4次及以上”的人数．
