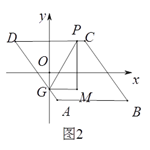Question

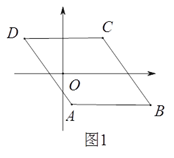
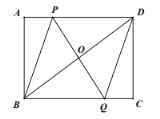
【题目】如图,矩形中,点是线段上一动点, 为的中点, 的延长线交BC于.

(1)求证: ;

(2)若,,从点出发,以l的速度向运动(不与重合).设点运动时间为,请用表示的长;并求为何值时,四边形是菱形.

Answer 1

【答案】(1)证明见解析；(2) PD=8-t，运动时间为秒时，四边形PBQD是菱形．

【解析】

(1)先根据四边形ABCD是矩形，得出AD∥BC，∠PDO=∠QBO，再根据O为BD的中点得出△POD≌△QOB，即可证得OP=OQ；

(2)根据已知条件得出∠A的度数，再根据AD=8cm，AB=6cm，得出BD和OD的长，再根据四边形PBQD是菱形时，利用勾股定理即可求出t的值，判断出四边形PBQD是菱形．

(1)∵四边形ABCD是矩形，

∴AD∥BC，

∴∠PDO=∠QBO，

又∵O为BD的中点，

∴OB=OD，

在△POD与△QOB中，

，

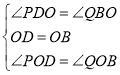∴△POD≌△QOB，

∴OP=OQ；

(2)PD=8-t，

∵四边形PBQD是菱形，

∴BP=PD= 8-t，

∵四边形ABCD是矩形，

∴∠A=90°，

在Rt△ABP中，由勾股定理得：AB2+AP2=BP2，

即62+t2=(8-t)2，

解得：t=，

即运动时间为秒时，四边形PBQD是菱形．