题目内容
如图△ABC中,AB=AC,角平分线AD、BD相交于点D.若∠ABC=80°,则∠ADB等于( )
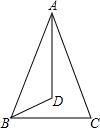
| A.100° | B.110° | C.120° | D.130° |

∵AB=AC,
∴∠C=∠ABC=80°,
∴∠BAC=180°-∠C-∠ABC=180°-80°-80°=20°
∵AD,BD分别是∠BAC,∠ABC的角平分线,
∴∠BAD=
∠BAC=
×20°=10°.
∠ABD=
×∠ABC=
×80°=40°.
∴∠ADB=180°-10°-40°=130°.
故选D.
∴∠C=∠ABC=80°,
∴∠BAC=180°-∠C-∠ABC=180°-80°-80°=20°
∵AD,BD分别是∠BAC,∠ABC的角平分线,
∴∠BAD=
| 1 |
| 2 |
| 1 |
| 2 |
∠ABD=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠ADB=180°-10°-40°=130°.
故选D.

练习册系列答案
相关题目
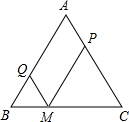 于P,交AB于Q.
于P,交AB于Q.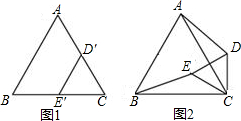
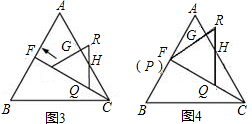
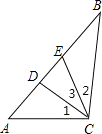
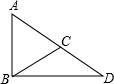 弧法”,如图所示,方法是:
弧法”,如图所示,方法是: