Question

如果等腰三角形的周长是25cm，一腰上的中线把三角形分成两个三角形的周长差是4cm．则这个等腰三角形的腰长为______．

Answer 1

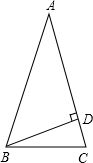
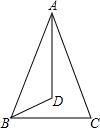
如图所示，等腰∉△ABC中，AB=AC，点D为AC的中点，设AB=AC=xcm，
∵点D为AC的中点，
∴AD=CD=

x

2

，BC=25-（AB+AC）=25-2x，
当△ABD的周长大于△BCD的周长时，
AB+AD+BD-（BC+CD+BD）=4，即x+

x

2

-（25-2x）-

x

2

=4，解得x=

29

3

cm；
当△BCD的周长大于△ABD的周长时，
则BC+CD+BD-（AB+AD+BD）=4，即25-2x+

x

2

-（x+

x

2

）=4，解得x=7cm．
综上所述，这个等腰三角形的腰长为7cm或

29

3

cm．
故答案为：7cm或

29

3

cm．