题目内容
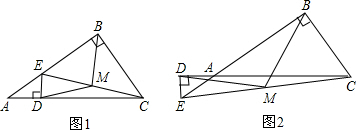
如图,在Rt△ABC中,∠ACB=90°,AC=AE,BC=BD,则∠ACD+∠BCE=______.
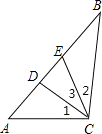

如图
解法一:设∠ACD=∠1,∠BCE=∠2,∠DCE=∠3.
∵AC=AE,
∴∠AEC=∠1+∠3.
∵BC=BD,
∴∠BDC=∠2+∠3.
两式相加得∠AEC+∠BDC=(∠1+∠2+∠3)+∠3=90°+∠3.
又在△DCE中∠DEC+∠EDC+∠3=180°.
∴90°+2∠3=180°,
∴∠3=45°,
∴∠1+∠2=45°.
解二:∵∠ACE是等腰△ACE的底角,
∴∠ACE=∠1+∠3=90°-
,
同理:∠2+∠3=90°-
,
∵∠1+∠2+∠3=90°,
∴90°+∠3=180°-
(∠A+∠B),
∴∠3=90°-
(∠A+∠B)=45°,
∴∠1+∠2=45°.

解法一:设∠ACD=∠1,∠BCE=∠2,∠DCE=∠3.
∵AC=AE,
∴∠AEC=∠1+∠3.
∵BC=BD,
∴∠BDC=∠2+∠3.
两式相加得∠AEC+∠BDC=(∠1+∠2+∠3)+∠3=90°+∠3.
又在△DCE中∠DEC+∠EDC+∠3=180°.
∴90°+2∠3=180°,
∴∠3=45°,
∴∠1+∠2=45°.
解二:∵∠ACE是等腰△ACE的底角,
∴∠ACE=∠1+∠3=90°-
| ∠A |
| 2 |
同理:∠2+∠3=90°-
| ∠B |
| 2 |
∵∠1+∠2+∠3=90°,
∴90°+∠3=180°-
| 1 |
| 2 |
∴∠3=90°-
| 1 |
| 2 |
∴∠1+∠2=45°.


练习册系列答案
相关题目
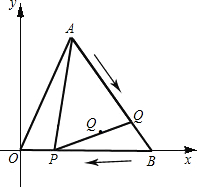 点Q从A点出发沿AB向终点B运动.两点同时出发,速度均为每秒1个单位,设从出发起运动了xs.
点Q从A点出发沿AB向终点B运动.两点同时出发,速度均为每秒1个单位,设从出发起运动了xs.