题目内容
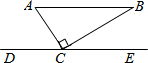
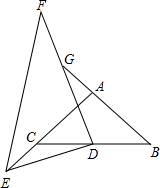
如图,△ABC是等腰直角三角形,△DEF是一个含30°角的直角三角形,将D放在BC的中点上,转动△DEF,设DE,DF分别交AC,BA的延长线于E,G,则下列结论:
①AG=CE
②DG=DE
③BG-AC=CE
④S△BDG-S△CDE=
S△ABC
其中总是成立的是______(填序号)
①AG=CE
②DG=DE
③BG-AC=CE
④S△BDG-S△CDE=
| 1 |
| 2 |
其中总是成立的是______(填序号)

连接AD.
∵△ABC是等腰直角三角形,D为BC的中点,
∴AD⊥BC,AD平分∠BAC,
∴∠ADB=∠ADC=90°,∠ACD=∠B=∠CAD=∠BAD=45°,CD=BD=AD,
∵∠EDF=90°,
∴∠ADG=∠EDC,∠ECD=∠GAD=135°,
∴在△ECD和△GAD中,
∴△ECD≌△GAD(AAS),
∴AG=CE,DG=DE,
∵AB=AC,
∴BG-AC=BG-AB=AG,
∵AG=CE,
∴BG-AC=CE,
∵△ECD≌△GAD,
∴S△ECD=S△GAD,
∵△ABC为等腰直角三角形,AD为斜边上的高,
∴S△ABC=2SADB,
∴S△BDG-S△CDE=S△BDG-S△ADG=S△ADB,
∴S△BDG-S△CDE=
S△ABC,
∴总上结论①②③④项均成立.
故答案为①②③④.

∵△ABC是等腰直角三角形,D为BC的中点,
∴AD⊥BC,AD平分∠BAC,
∴∠ADB=∠ADC=90°,∠ACD=∠B=∠CAD=∠BAD=45°,CD=BD=AD,
∵∠EDF=90°,
∴∠ADG=∠EDC,∠ECD=∠GAD=135°,
∴在△ECD和△GAD中,
|
∴△ECD≌△GAD(AAS),
∴AG=CE,DG=DE,
∵AB=AC,
∴BG-AC=BG-AB=AG,
∵AG=CE,
∴BG-AC=CE,
∵△ECD≌△GAD,
∴S△ECD=S△GAD,
∵△ABC为等腰直角三角形,AD为斜边上的高,
∴S△ABC=2SADB,
∴S△BDG-S△CDE=S△BDG-S△ADG=S△ADB,
∴S△BDG-S△CDE=
| 1 |
| 2 |
∴总上结论①②③④项均成立.
故答案为①②③④.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目