题目内容
【题目】如图,矩形ABCD中,AD=5,AB=6,点E为DC上一个动点,把△ADE沿AE折叠,点F为CD上一个动点,把△BCF沿BF折叠,当点D的对应点和点C的对应点都落在点D′处时,EF的长为 . 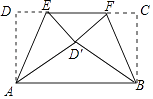
【答案】![]()
【解析】解:根据题意得△ADE≌△AD′E,△BCF≌△BD′F, ∴AD=AD′,BD′=BC,∠DAE=∠D′AE,∠CBF=∠D′BF,
∵矩形ABCD中,AD=BC,∠DAB=∠CBA=90°,
∴AD′=BD′,
∴∠D′AB=∠D′BA,
∴∠EAD′=∠FBD′,
∴△AED′≌△BFD′,
∴ED′=FD′,
∴DE=CF,
设DE=CF=D′E=D′F=x,
∴EF=6﹣2x,
过D′作D′G⊥AB于G反向延长交EF于H,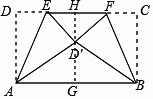
∵CD∥AB,
∴GH⊥EF,
则EH=HF=3﹣x,HG=AD=5,
∴D′G= ![]() =4,
=4,
∴HD′=1,
∵EH2+HD′2=ED′2 ,
∴(3﹣x)2+1=x2 ,
∴x= ![]() ,
,
∴EF= ![]() .
.
【考点精析】解答此题的关键在于理解矩形的性质的相关知识,掌握矩形的四个角都是直角,矩形的对角线相等,以及对翻折变换(折叠问题)的理解,了解折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目