题目内容
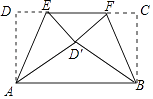
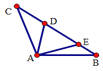
【题目】如图△ABC中,AB=AC,∠BAC=120°,∠DAE=60°,BE=4,CD=6,则DE的长为________.
【答案】![]()
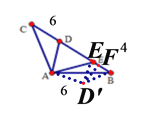
【解析】分析:把△ADC绕点A顺时针旋转120°得到△AD′B,再结合条件可证明△AD′E≌△ADE,可得ED′=ED,过D′作DF⊥BE于点F,可求得EF和D′F的长,在Rt△D′FE中可求得ED′,
则可求得ED.
详解:∵AB=AC,
∴可把△ADC绕点A顺时针旋转120°得到△AD′B,
∴BD′=DC=6,AD′=AD,∠D′AB=∠DAC,
∵∠BAC=120°,∠EAD=60°,
∴∠BAE+∠DAC=60°,
∴∠D′AE=∠D′AB+∠BAE=60°,
在△D′AE和△DAE中
AD'=AD,
∠D'AE=∠DAE,
AE=AE,
∴△D′AE≌△DAE(SAS),
∴D′E=DE,
过D′作DF⊥BE于点F,连接D′F,
∵AB=AC,∠BAC=120°,
∴∠ABC=∠C=∠D′BA=30°,
∴∠D′BF=60°,
∴∠BD′F=30°,
∴BF=![]() BD′=3,D′F=3
BD′=3,D′F=3![]() ,
,
∵BE=4,
∴FE=BE-BF=1,
在Rt△D′FE中,由勾股定理可得D′E=![]() ,
,
∴ED=![]() .
.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
【题目】某校九年级(1)班全体学生上周末进行体育测试的成绩(满分70分)统计如表:
成绩(分) | 45 | 50 | 55 | 60 | 65 | 68 | 70 |
人数(人) | 2 | 6 | 10 | 7 | 6 | 5 | 4 |
根据表中的信息判断,下列结论中错误的是( )
A. 该班一共有40名同学
B. 该班学生这次测试成绩的众数是55分
C. 该班学生这次测试成绩的中位数是60分
D. 该班学生这次测试成绩的平均数是59分