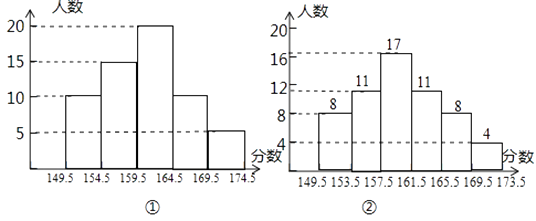
题目内容
【题目】阅读理解,回答下列问题:
![]()
![]()
![]()
(1)试猜想:1+3+5+7+9+…+2015+2017+2019的和是多少?
(2)推广:1+3+5+7+9+…+(2n-1)+(2n+1)的和是多少?
(3)计算:103+105+107+…+2017+2019.
【答案】(1)10102;(2)(n+1)2;(3)1018458.
【解析】
(1)由等式可知左边是连续奇数的和,右边是数的个数的平方,由此规律解答即可;
(2)由(1)的结论可知是(n+1)个连续奇数的和,得出结果;
(3)让从1加到2019这些连续奇数的和,减去从1加到101这些连续奇数的和即可.
由1+3=4=22
1+3+5=9=32
1+3+5+7=16=42
1+3+5+7+9=25=52
…
依此类推:第n个等式所代表的算式为:1+3+5+…+(2n-1)=n2;
(1)1+3+5+7+9+…+2015+2017+2019=10102;
(2)1+3+5+7+9+…+(2n-1)+(2n+1)=1+3+5+7+9+…+(2n-1)+[2(n+1)-1]=(n+1)2;
(3)103+105+107+…+2017+2019=(1+3+…2019)-(1+3+…+101)=10102-512=1018458.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
【题目】如图,某计算装置有一數据输入口A和一运算结果的输出口B,表格中是小明输入的一些数据和这些数据经该装置计算后输出的相应结果,按照这个计算装置的计算规律,若输入的数是10,则输出的数是( )
A | 1 | 2 | 3 | 4 | 5 |
B | 0 | 3 | 8 | 15 | 24 |
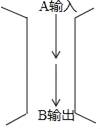
A. 99 B. 100 C. 101 D. 102