题目内容
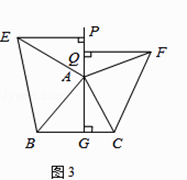
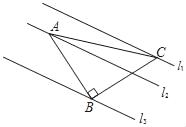
【题目】如图,△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为2,l2,l3之间的距离为3,则AC的长是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】分析:
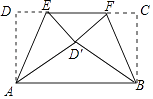
如下图,过点A作AD⊥l3于点D,过点C作CE⊥l3于点E,则由题意可得AD=3,CE=5,再证△ABD≌△BCE即可得到BD=CE=5,从而在Rt△ADB中由勾股定理可得AB=![]() ,这样结合△ABC中,∠ABC=90°,AB=BC即可得到AC=
,这样结合△ABC中,∠ABC=90°,AB=BC即可得到AC=![]() .
.
详解:
如下图,过点A作AD⊥l3于点D,过点C作CE⊥l3于点E,
∴∠ADB=∠ABC=∠CEB=90°,
∴∠BAD+∠ABD=90°,∠ABD+∠CBE=90°,
∴∠BAD=∠CBE,
又∵AB=BC,
∴△ABD≌△BCE,
∴BD=CE,
∵由题意可得:CE=5,AD=2,
∴BD=5,
∴在Rt△ABD中由勾股定理可得AB=![]() ,
,
∵△ABC中,∠ABC=90°,AB=BC,
∴AC=![]() .
.
故选B.

练习册系列答案
相关题目
【题目】如图,某计算装置有一數据输入口A和一运算结果的输出口B,表格中是小明输入的一些数据和这些数据经该装置计算后输出的相应结果,按照这个计算装置的计算规律,若输入的数是10,则输出的数是( )
A | 1 | 2 | 3 | 4 | 5 |
B | 0 | 3 | 8 | 15 | 24 |
A. 99 B. 100 C. 101 D. 102