题目内容
【题目】定义:有一组对角互补的凸四边形叫做“对补四边形”,性质:“对补四边形”一定是圆内接四边形.
(1)概念理解:请你根据上述描述定义举一个“对补四边形”的例子;
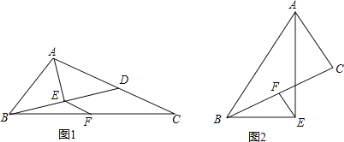
(2)问题探究:如图1,在对补四边形ABCD中,如果∠A=∠C,试探究AB、AD、BC、CD之间的数量关系,并说明理由;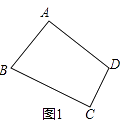
(3)应用拓展:如图2,在四边形ABCD中,AB≠BC,∠A=∠C=90°,连接BD,将△BCD沿BD折叠,得到△BFD.
①连接AF,四边形ABDF是对补四边形吗?请说明理由;
②若AB=1,BD=2,且BF把△ABD分成两个三角形的面积比为1:2,请求出CD的长.
【答案】
(1)解:矩形是“对补四边形”
(2)解:AB2+AD2=BC2+CD2;理由如下:
连接BD,如图1所示:
∵四边形ABCD是“对补四边形”,
∴∠A=+∠C=90°,
∵∠A=∠C,
∴∠A=∠C=90°,
∴AB2+AD2=BD2,BC2+CD2=BD2,
∴AB2+AD2=BC2+CD2
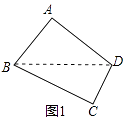
(3)解:①四边形ABDF是对补四边形,理由如下:
∵∠BAD=∠C=90°,
∴∠BAD+∠C=180°,
∴A、B、C、D四点共圆,
由折叠的性质得:∠BFD=∠BAD=90°,
∴点F在A、B、C、D四点共圆的这个圆上,
∴∠BAF+∠BDF=180°,
∴四边形ABDF是对补四边形;
②∵AB=1,BD=2,∠BAD=90°,
∴sin∠ADB= ![]() =
= ![]() ,AD=
,AD= ![]() =
= ![]() ,
,
∴∠ADB=30°,
∴∠ABD=60°,
设AD与BF交于点P,作PM⊥BD于M,如图2所示:
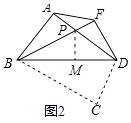
∵BF把△ABD分成两个三角形的面积比为1:2,
∴AP:PD=1:2,或PD:AP=1:2,
,当AP:PD=1:2时,AP= ![]() AD=
AD= ![]() ,PD=
,PD= ![]() AD=
AD= ![]() ,
,
∴∠ADB=30°,
∴PM= ![]() PD=
PD= ![]() =PA,
=PA,
∴∠ABP=∠DBP= ![]() ∠ABD=30°,
∠ABD=30°,
∵∠BFD=90°,
∴DF= ![]() BD=1,
BD=1,
∴CD=DF=1;
当PD:AP=1:2时,PD= ![]() AD=
AD= ![]() ,AP=
,AP= ![]() AD=
AD= ![]() ,
,
∴BP= ![]() =
= ![]() ,
,
∵∠BAD=∠BFD=90°,∠APB=∠FPD,
∴△ABP∽△FDP,
∴ ![]() ,即
,即  ,
,
解得:FD= ![]() ,
,
∴CD=FD= ![]() ;
;
综上所述:CD的长为1或 ![]() .
.
【解析】(1)由矩形的性质容易得出矩形是“对补四边形”
(2)连接BD,由“对补四边形”的定义得出∠A=+∠C=90°,由已知得出∠A=∠C=90°,由勾股定理得出AB2+AD2=BD2,BC2+CD2=BD2,即可得出结论;
(3)①证明A、B、C、D四点共圆,由折叠的性质得:∠BFD=∠BAD=90°,证出点F在A、B、C、D四点共圆的这个圆上,由圆内接四边形的性质得出∠BAF+∠BDF=180°,即可得出结论;②由三角函数得出sin∠ADB= ![]() =
= ![]() ,由勾股定理求出AD=
,由勾股定理求出AD= ![]() =
= ![]() ,得出∠ADB=30°,由直角三角形的性质得出∠ABD=60°,设AD与BF交于点P,作PM⊥BD于M,由已知得出AP:PD=1:2,或PD:AP=1:2,分别求出DF的长,即可得出CD的长.
,得出∠ADB=30°,由直角三角形的性质得出∠ABD=60°,设AD与BF交于点P,作PM⊥BD于M,由已知得出AP:PD=1:2,或PD:AP=1:2,分别求出DF的长,即可得出CD的长.
【考点精析】认真审题,首先需要了解相似三角形的应用(测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解).