题目内容
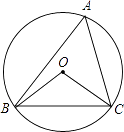
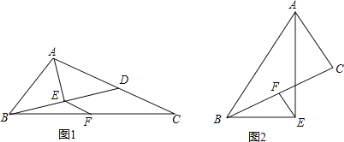
【题目】如图,在△ABC中,AE平分∠BAC,BE⊥AE于点E,点F是BC的中点.
(1)如图1,BE的延长线与AC边相交于点D,求证:EF=![]() (AC﹣AB);
(AC﹣AB);
(2)如图2,请直接写出线段AB、AC、EF之间的数量关系。
【答案】(1)详见解析;(2)EF=![]() (AB-AC),理由详见解析.
(AB-AC),理由详见解析.
【解析】
(1)先证明AB=AD,根据等腰三角形的三线合一,推出BE=ED,根据三角形的中位线定理即可解决问题;
(2)先证明AB=AP,根据等腰三角形的三线合一,推出BE=ED,根据三角形的中位线定理即可解决问题.
(1)证明 如图1中,

∵AE⊥BD,
∴∠AED=∠AEB=90°,
∴∠BAE+∠ABE=90°,∠DAE+∠ADE=90°,
∵∠BAE=∠DAE,
∴∠ABE=∠APE,
∴AB=AD,∵AE⊥BD,
∴BE=DE,∵BF=FC,
∴EF=![]() DC=
DC=![]() (AC-AD)=
(AC-AD)=![]() (AC-AB).
(AC-AB).
(2)结论:EF=![]() (AB-AC),
(AB-AC),
理由:如图2中,延长AC交BE的延长线于P.

∵AE⊥BP,
∴∠AEP=∠AEB=90°,
∴∠BAE+∠ABE=90°,∠PAE+∠APE=90°,
∵∠BAE=∠PAE,
∴∠ABE=∠ADE,
∴AB=AP,
∵AE⊥BD,
∴BE=PE,
∵BF=FC,
∴EF=![]() PC=
PC=![]() (AP-AC)=
(AP-AC)=![]() (AB-AC).
(AB-AC).

练习册系列答案
相关题目