题目内容
【题目】如图,AB是⊙O的直径,点P是弦AC上一动点(不与A,C重合),过点P作PE⊥AB,垂足为E,射线EP交 ![]() 于点F,交过点C的切线于点D.
于点F,交过点C的切线于点D. 
(1)求证:DC=DP;
(2)若直径AB=12cm,∠CAB=30°, ①当E是半径OA中点时,切线长DC=cm:
②当AE=cm时,以A,O,C,F为顶点的四边形是菱形.
【答案】
(1)证明:连接OC.
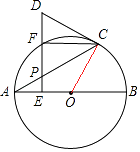
∵CD是⊙O的切线,
∴∠OCD=90°,
∵OA=OC,
∴∠OAC=∠OCA,
∵PE⊥AB,
∴∠PEA=90°,
∴∠OAC+∠APE=90°,∠OCA+∠PCD=90°,
∴∠APE=∠PCD,
∵∠APE=∠CPD,
∴∠PCD=∠CPD,
∴DC=DP.
(2)4 ![]() ;3
;3
【解析】解:(2)①连接BC, 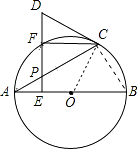
∵AB是直径,
∴∠ACB=90°
∵∠A=30°,AB=12,
∵AC=ABcos30°=6 ![]() ,
,
在Rt△APE中,∵AE= ![]() OA=3,
OA=3,
∴AP=AE÷cos30°=2 ![]() ,
,
∴PC=AC﹣AP=4 ![]() ,
,
∵∠APE=∠DPC=60°,DP=DC,
∴△DPC是等边三角形,
∴DC=4 ![]() ,
,
所以答案是4 ![]()
. ②当AE=EO时,四边形AOCF是菱形.
理由:连接AF、OF.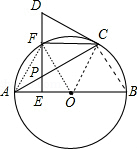
∵AE=EO,FE⊥OA,
∴FA=FO=OA,
∴△AFO是等边三角形,
∴∠FAO=60°,∵∠CAB=30°,
∴∠FAC=30°,∠FOC=2∠FAC=60°,
∴△FOC是等边三角形,
∴CF=CO=OA=AF,
∴四边形AOCF是菱形,
∴AE=3cm时,四边形AECF是菱形.
所以答案是3.
【考点精析】本题主要考查了菱形的判定方法和垂径定理的相关知识点,需要掌握任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形;垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧才能正确解答此题.