题目内容
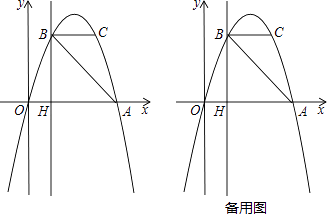
【题目】用小立方块搭一几何体,使得它的从正面看和从上面看形状图如图所示,这样的几何体最少要______个立方块,最多要_______个立方块.

【答案】![]()
![]()
【解析】
由几何体的主视图和俯视图可知,该几何体的主视图的第一列3个正方形中每个正方形所在位置最多均可有2个小立方块,最少一个正方形所在位置有2个小立方块,其余2个所在位置各有1个小立方块;主视图的第二列2个小正方形中,每个小正方形所在位置最多均可有3个小立方体,最少一个正方形所在位置有3个小立方块,另1个所在位置有1个小立方块;主视图的第三列1个小正方形所在位置只能有1个小立方块.
观察图象可知:这样的几何体最少需要(2+1+1)+(3+1)+1=9(个)小立方块;
最多需要3×2+2×3×1=13(个)小立方块.
故答案为:9,13.

练习册系列答案
相关题目
【题目】两会期间,记者随机抽取参会的部分代表,对他们某天发言的次数进行了统计,其结果如表,并绘制了如图所示的两幅不完整的统计图,请结合图中相关数据回答下列问题:
发言次数n | |
A | 0≤n<3 |
B | 3≤n<6 |
C | 6≤n<9 |
D | 9≤n<12 |
E | 12≤n<15 |
F | 15≤n<18 |
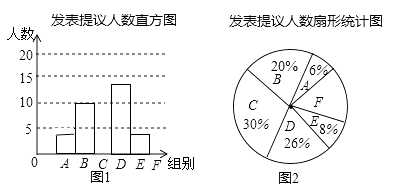
(1)求得样本容量为 , 并补全直方图;
(2)如果会议期间组织1700名代表参会,请估计在这一天里发言次数不少于12次的人数;
(3)已知A组发表提议的代表中恰有1为女士,E组发表提议的代表中只有2位男士,现从A组与E组中分别抽一位代表写报告,请用列表法或画树状图的方法,求所抽的两位代表恰好都是男士的概率.