��Ŀ����
����Ŀ���ۺ���̽��
�Ķ����ϣ�
������ѧϰ��������һ����Ҫ���ߣ��κ��������������������ϵĵ��ʾ�������ܹ��������ν�ϵķ������һЩ���⣮���磬�����������������϶�Ӧ�ĵ�֮��ľ�����������������IJ�ľ���ֵ��ʾ��
�������ϣ�������3��1��Ӧ������֮��ľ���Ϊ|3��1|=2��
�������ϣ�������5�멁2��Ӧ������֮��ľ���Ϊ|5������2��|=7��
�������ϣ���������2��3��Ӧ������֮��ľ���Ϊ|��2��3|=5��
�������ϣ���������8�멁5��Ӧ������֮��ľ���Ϊ|��8������5��|=3������
��ͼ1����������������a��Ӧ�ĵ�Ϊ��A��������b��Ӧ�ĵ�Ϊ��B��A��B����֮��ľ����ʾΪ|a��b|��|b��a|����Ϊ|AB|=|a��b|=|b��a|��

������⣺
(1)��������������10�멁5��Ӧ������֮��ľ�������� ����������������x�멁5��Ӧ������֮��ľ����ú�x��ʽ�ӱ�ʾΪ�� ������������������x�멁1��Ӧ������A��B֮��ľ���|AB|=2����x������ ����
��ϵ�ع㣺
(2)��ͼ2����M��N��P�������ϵ����㣬��M��ʾ����Ϊ4����N��ʾ����Ϊ��2������P��ʾ����Ϊx��
���A��B��������ѡһ��������ѡ���� ���⣮
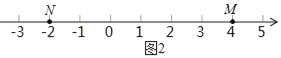
A��������P�ڵ�M��N����֮�䣬��|PM|+|PN|=�� ����
����|PM|=2|PN|������P����M�ľ�����ڵ�P����N�ľ����2������x������ ����
B��������P�ڵ�M��N֮�䣬��|x+2|+|x��4|=�� ����
��|x+2|+|x��4|�T10����x=�� ����
�ڸ����Ķ����ϼ���������Ľ����|x+2|+|x|+|x��2|+|x��4|����Сֵ������ ����
���𰸡�(1)5�� |x+5|��1��3��(2)A����6����0��-8��B����6�� 6��4����8��
��������
(1)����������A��B����֮��ľ���|AB|=|a-b|��������ֵ���þ���ֵ�������������ľ��룻
(2)A���ٵ�P��M��N����֮�䣬|PM|+|PN|����M��N֮��ľ��룻�ڷֵ�P��M��N֮��͵�P��N������������
B�������������Ͼ���ֵ�ļ���������н������-2��x��4ʱ��ԭʽ������Сֵ8.
�⣺(1)���ݾ���ֵ�Ķ��壺
��������������10�멁5��Ӧ������֮��ľ������5��
������������x�멁5��Ӧ������֮��ľ����ú�x��ʽ�ӱ�ʾΪ|x+5|��
A��B֮��ľ���|AB|=2����x����1��3��
(2)A��������P�ڵ�M��N����֮�䣬��|PM|+|PN|=6��
����|PM|=2|PN|��P��MN֮�����N��࣬��x����0��-8��
B��������P�ڵ�M��N֮�䣬��|x+2|+|x��4|=6��
��|x+2|+|x��4|�T10����x=6��4��
��|x+2|+|x|+|x��2|+|x��4|����Сֵ��
����x��4��2��0����2֮��������С�������Сֵ8��
�ʴ�Ϊ��(1)5�� |x+5|��1��3��(2)A����6����0��-8��B����6�� 6��4����8��

 ��У����ϵ�д�
��У����ϵ�д�