��Ŀ����
����Ŀ����ͼ��������y=ax2+bx��A��4��0����B��1��3�����㣬��C��B���������ߵĶԳ���Գƣ�����B��ֱ��BH��x�ᣬ��x���ڵ�H��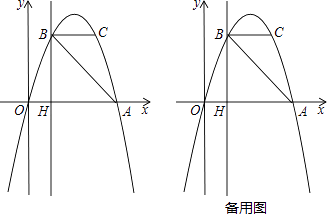
��1���������ߵı���ʽ��
��2��ֱ��д����C�����꣬�������ABC�������
��3����P����������һ���㣬��λ�ڵ������ޣ�����ABP�����Ϊ6ʱ�������P�����ꣻ
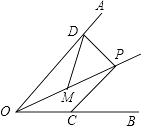
��4������M��ֱ��BH���˶�����N��x�����˶�����CM=MN���ҡ�CMN=90��ʱ�����ʱ��CMN�������
���𰸡�
��1��
�⣺�ѵ�A��4��0����B��1��3������������y=ax2+bx�У��� ![]() ��ã�
��ã� ![]() ��
��
�������߱���ʽΪ��y=��x2+4x
��2��
�⣺�����߶Գ���Ϊx=�� ![]() =2��
=2��
�ߵ�C��B���������ߵĶԳ���Գƣ���B������Ϊ��1��3����
���C��������3��3����
��BC=2��
��S��ABC= ![]() ��2��3=3
��2��3=3
��3��
�⣺��P����PD��BH��BH�ڵ�D��
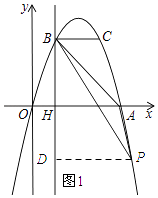
���P��m����m2+4m����
��������ã�BH=AH=3��HD=m2��4m��PD=m��1��
��S��ABP=S��ABH+S�ı���HAPD��S��BPD����6= ![]() ��3��3+
��3��3+ ![]() ��3+m��1����m2��4m����
��3+m��1����m2��4m���� ![]() ��m��1����3+m2��4m����
��m��1����3+m2��4m����
�����ã�3m2��15m=0��
��ã�m1=0����ȥ����m2=5��
���P������5����5��
��4��
�⣺��CM=MN���ҡ�CMN=90��ʱ����������ۣ�
�ٵ���M��x���Ϸ�ʱ����ͼ2��ʾ��
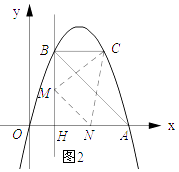
�ߡ�CMN=90�㣬
���BMC+��NMH=90�㣮
�֡ߡ�BMC+��BCM=90�㣬
���NMH=��BCM��
�ڡ�BCM�͡�HMN��  ��
��
���CBM�ա�MHN��
��BC=MH=2��BM=HN=3��2=1��
��M��1��2����N��2��0����
�ɹ��ɶ����ã�MC= ![]() =
= ![]() ��
��
��S��CMN= ![]() ��
�� ![]() ��
�� ![]() =
= ![]() ��
��
�ڵ���M��x���·�ʱ����ͼ3��ʾ������ֱ��������Rt��NEM��Rt��MDC
�ߡ�NMC=90�㣬
���NME+��CMD=90�㣮
�ߡ�ENM+��EMN=90�㣬
���CMD=��ENM��
��Rt��NEM��Rt��MDC�� 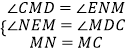
��Rt��NEM��Rt��MDC��
��EM=CD=5��MD=ME=2��
�ɹ��ɶ����ã�CM= ![]() =
= ![]() ��
��
��S��CMN= ![]() ��
�� ![]() ��
�� ![]() =
= ![]() ��
��
������������CMN������� ![]() ��
�� ![]()
����������1���ѵ�A��4��0����B��1��3������������y=ax2+bx�У����a��b��ֵ���Ӷ��õ������ߵĽ���ʽ����2������������߶Գ���Ϊx=2���ɵ�B������ɵõ���C�����꣬�Ӷ��õ�BC�ij���Ȼ�����������ε������ʽ��⼴�ɣ�3����P����PD��BH��BH�ڵ�D�����P��m����m2+4m������BH=AH=3��HD=m2��4m��PD=m��1��Ȼ������S��ABP=S��ABH+S�ı���HAPD��S��BPD �� �г�����m�ķ��̣��Ӷ������m��ֵ���ǿ���õ�P�����ꣻ��4���ٵ���M��x���Ϸ�ʱ����֤�������Ρ�CBM�ա�MHN���Ӷ������BC=MH=2��BM=1�����ǿɵõ���M��N�����꣬Ȼ�����ݹ��ɶ������MC�ij���������������ε������ʽ��⼴�ɣ�����ͼ3��ʾ������M��x���·�ʱ������M��ƽ����x���ֱ�ߣ�Ȼ��ֱ����N�͵�C��x��Ĵ��ߣ��Ӷ��ɹ����ֱ��������Rt��NEM��Rt��MDC������������֤��Rt��NEM��Rt��MDC������ȫ�������ε����ʿɵõ�EM=CD=5��MD=ME=2��Ȼ�����ݹ��ɶ��������CM�ij���������������ε������ʽ��⼴�ɣ�
�����㾫����������Ĺؼ�����������κ��������ʵ����֪ʶ�����������ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С��

 ���Ž�������С״Ԫϵ�д�
���Ž�������С״Ԫϵ�д�