Question

【题目】定义：在三角形中，若有两条中线互相垂直，则称该三角形为中垂三角形．

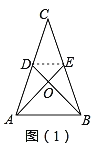
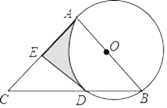
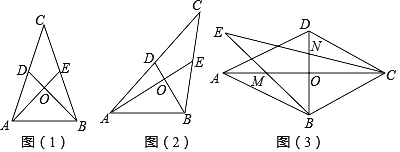
（1）如图（1），△ABC是中垂三角形，BD，AE分别是AC，BC边上的中线，且BD⊥AE于点O，若∠BAE＝45°，求证：△ABC是等腰三角形．

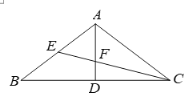
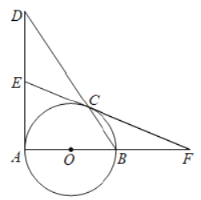
（2）如图（2），在中垂三角形ABC中，AE，BD分别是边BC，AC上的中线，且AE⊥BD于点O，猜想AB2，BC2，AC2之间的数量关系，并加以证明．

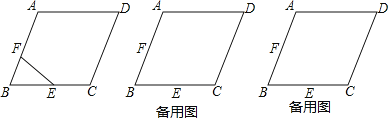
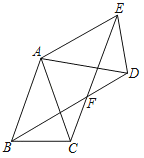
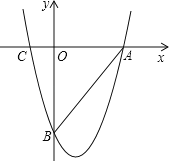
（3）如图（3），四边形ABCD是菱形，对角线AC，BD交于点O，点M，N分别是OA，OD的中点，连接BM，CN并延长，交于点E．

①求证：△BCE是中垂三角形；

②若，请直接写出BE2+CE2的值．

Answer 1

【答案】（1）详见解析；（2）AC2+BC2＝5AB2，证明详见解析；（3）①详见解析；②40．

【解析】

（1）先判断出DE是△ABC的中位线，进而判断出△AOD≌△BOE（SAS），即可得出结论；

（2）先判断出AC＝2AD，BC＝2BE，再借助勾股定理，即可得出结论；

（3）①先判断出MN∥BC，MN=BC，即可得出结论；

②同（2）的方法即可判断出

（1）证明：如图（1），∵BD⊥AE，∠BAE＝45°，

∴∠ABD＝45°．

连接DE，

由题意可得，AC＝2AD，BC＝2BE，DE是△ABC的中位线，

∴DE∥AB，

∴∠AED＝∠BAE＝∠ABD＝∠EDB＝45°，

∴OD＝OE，OA＝OB．

又∵∠AOD＝∠BOE＝90°，

∴△AOD≌△BOE（SAS），

∴AD＝BE，

∴AC＝BC，

∴△ABC是等腰三角形；

（2）AC2+BC2＝5AB2．

证明：如图（2），连接DE，∵AE，BD分别是边BC，AC上的中线，

∴AC＝2AD，BC＝2BE，DE=AB，

∴AC2＝4AD2，BC2＝4BE2，DE2=AB2，

在Rt△AOD中，AD2＝OD2+OA2，

在Rt△BOE中，BE2＝OB2+OE2，

∴AC2+BC2＝4（AD2+BE2）＝4（OA2+OD2+OB2+OE2）＝4(AB2+DE2)=4(AB2+AB2)=5AB2；

（3）①证明：如图（3），连接MN．

∵点M，N分别是OA，OD的中点，

∴MN是△AOD的中位线，

则MN∥AD，且MN=AD．

∵四边形ABCD是菱形，

∴CM⊥BN，AD＝BC，且AD∥BC，

∴MN∥BC，MN=BC，

∴EM＝MB，EN＝AC，

∴CM，BN是△BCE的中线，

∴△BCE是中垂三角形．

②∵AB＝2，

同（2）的方法得，BE2+CE2＝5AB2＝5×（2）2＝40．