题目内容
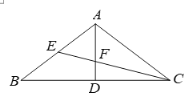
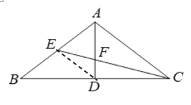
【题目】如图,在△ABC中,AB=AC=5,BC=8,中线AD、CE相交于点F,则AF的长为_______.
【答案】2
【解析】
连接DE,由中线的性质可知:AD⊥BC,BD=CD=4,由勾股定理得出AD=3,设AF=x,则DF=AD-AF=3-x,再推导出DE是△ABC的中位线,进而由相似三角形的判定证出△DEF∽△ACF,进而将相应数据代入对应线段成比例的公式解方程即可.
解:如图,连接DE,
∵AB=AC=5,BC=8,AD是BC边上的中线,
∴AD⊥BC,BD=CD=4,
在Rt△ABD中, ![]() ,
,
设AF=x,则DF=AD-AF=3-x,
∵CE是AB边上的中线,
∴AE=BE,
∴DE是△ABC的中位线,
∴DE∥AC,DE=![]() AC,
AC,
∴△DEF∽△ACF,
∴![]() ,
,
∴AF=2DF,
∴![]()
解得:![]()
∴AF=2.
故答案为:2

【题目】某超市为了回惯顾客,计划于周年店庆当天举行抽奖活动.凡是购物金额达到m元及以上的顾客,都将获得抽奖机会.规则如下:在一个不透明袋子里装有除数字标记外其它完全相同的4个小球,数字标记分别为“a” 、“b”、“c”、“0” (其中正整数a、b、c满足a+b+c=30且a>15).顾客先随机摸出一球后不放回,再摸出第二球,则两球标记的数字之和为该顾客所获奖励金额(单位:元)、经调查发现,每日前来购物的顾客中,购物金额及人数比例如下表所示:
购物金额x (单位:元) | 0<x<100 | 100≤x<200 | 200≤x<300 | x≥300 |
人数比例 |
|
|
|
|
现预计活动当天购物人数将达到200人.
(1)在活动当天,某顾客获得抽奖机会,试用画树状图或列表的方法,求该顾客获得a元奖励金的概率;
(2)以每位抽奖顾客所获奖励金的平均数为决策依据,超市设定奖励总金额不得超过2000元,且尽可能让更多的顾客参与抽奖活动,问m应定为100元?200元?还是300元?请说明理由.
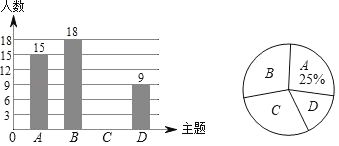
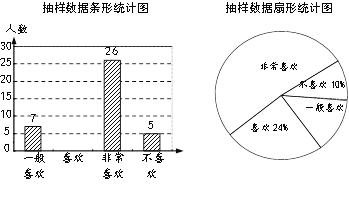
【题目】在信息快速发展的社会,“信息消费”已成为人们生活的重要组成部分.某高校组织课外小组在郑州市的一个社区随机抽取部分家庭,调查每月用于信息消费的金额,根据数据整理成如图所示的不完整统计表和统计图.已知A,B两组户数频数直方图的高度比为1:5.
月信息消费额分组统计表
组别 | 消费额(元) |
A | 10≤x<100 |
B | 100≤x<200 |
C | 20≤x<300 |
D | 300≤x<400 |
E | x≥400 |
请结合图表中相关数据解答下列问题:
(1)这次接受调查的有 户;
(2)在扇形统计图中,“E”所对应的圆心角的度数是 ;
(3)请你补全频数直方图;
(4)若该社区有2000户住户,请估计月信息消费额不少于200元的户数是多少?