题目内容
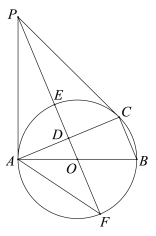
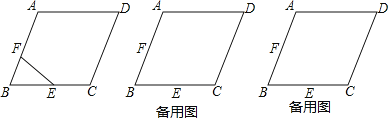
【题目】已知,如图,在边长为10的菱形ABCD中,cos∠B=![]() ,点E为BC边上的中点,点F为边AB边上一点,连接EF,过点B作EF的对称点B′,
,点E为BC边上的中点,点F为边AB边上一点,连接EF,过点B作EF的对称点B′,
(1)在图(1)中,用无刻度的直尺和圆规作出点B′(不写作法,保留痕迹);
(2)当△EFB′为等腰三角形时,求折痕EF的长度.
(3)当B′落在AD边的中垂线上时,求BF的长度.
【答案】(1)尺规作图见解析;(2)EF=5或![]() 或
或![]() ;(3)
;(3)![]() .
.
【解析】
试题(1)分别以F、E为圆心,FB、EB为半径画弧,两弧交于点B,B即为所求;
(2)分情况①当BE=EF时,②BE=BF时,③EF=BF时讨论即可;
(3)连接BB,FE,可知BB⊥FE,依据翻折及勾股定理即可解得.
试题解析:(1)尺规作图:
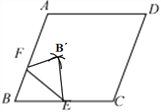
(2)由翻折知:△FBE≌△FBE,
∴BE=BE,BF=BF,
∵点E为BC边上的中点,
∴BE=BE=5,
① 当BE=EF时,EF=5,
②当BE=BF时,过点F作FG⊥BE于点G,
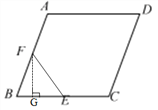
在Rt△FBG中,BE=BF=5,cos∠B=![]() ,
,
∴BG=![]() ,GE=BE-BG=
,GE=BE-BG=![]() ,
,
FG=![]() ,
,
在Rt△FEG中,FE=![]() ;
;
③当EF=BF时,
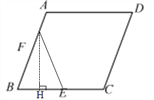
过点F作FH⊥BE于点H,BH=![]() BE=
BE=![]() ,
,
在Rt△FBH中, cos∠B=![]() ,
,
∴BF=BH×![]() =
=![]() ,
,
∴EF=![]() ,
,
综上:EF=5或![]() 或
或![]() .
.
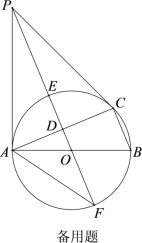
(3)
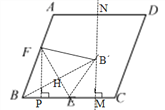
如图:连接BB,FE,交点 为H,
则BB⊥FE,
∵AN=DN=BE=CE=5,
∴BM=4,MN=![]() ,B B=
,B B=![]() ,
,
BH=![]() ,
,
∴BF=BF=![]() .
.

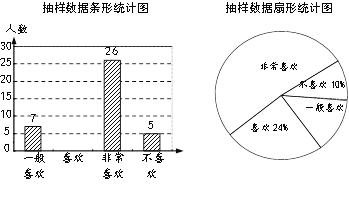
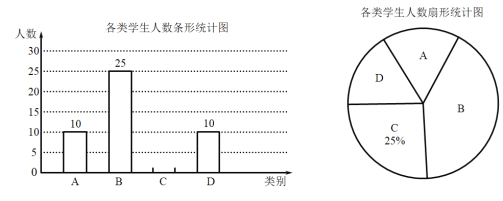
【题目】在信息快速发展的社会,“信息消费”已成为人们生活的重要组成部分.某高校组织课外小组在郑州市的一个社区随机抽取部分家庭,调查每月用于信息消费的金额,根据数据整理成如图所示的不完整统计表和统计图.已知A,B两组户数频数直方图的高度比为1:5.
月信息消费额分组统计表
组别 | 消费额(元) |
A | 10≤x<100 |
B | 100≤x<200 |
C | 20≤x<300 |
D | 300≤x<400 |
E | x≥400 |
请结合图表中相关数据解答下列问题:
(1)这次接受调查的有 户;
(2)在扇形统计图中,“E”所对应的圆心角的度数是 ;
(3)请你补全频数直方图;
(4)若该社区有2000户住户,请估计月信息消费额不少于200元的户数是多少?