题目内容
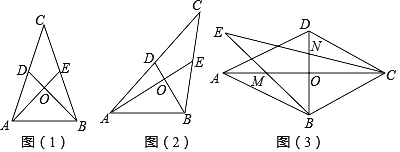
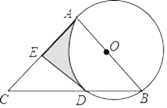
【题目】如图,AB是⊙O的直径,AC是⊙O的切线,切点为A,BC交⊙O于点D,点E是AC的中点.
(1)试判断直线DE与⊙O的位置关系,并说明理由.
(2)若⊙O半径为2,∠B=60°,求图中阴影部分的面积.
【答案】(1)直线DE与⊙O相切,理由见解析(2)4![]() -
-![]()
【解析】
(1)连接0E、OD,如图,根据切线的性质得∠OAC=90°,再证明△AOE≌△DOE得到∠ODE=∠OAE=90°,然后根据切线的判定定理得到DE为⊙0的切线
(2)先计算出四边形AEDO的面积,利用四边形的面积减去扇形的面积计算图中阴影部分的面积
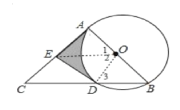
(1)直线DE与⊙O相切.理由如下:
连接OE、OD,如图,
∵AC是⊙O的切线,
∴.AB⊥AC,
∴∠OAC=90°,
∵点E是AC的中点,O点为AB的中点,
∴OE∥BC
∴.∠1=∠B,∠2=∠3
∵OB=OD
∴∠B=∠3
∴∠1=∠2,
在△AOE和△DOE中
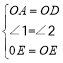
∴△AOE≌△DOE,
∴∠ODE=∠OAE=90°
∴OD⊥DE
∴DE为⊙O的切线;
(2)S![]() =AD×OE=
=AD×OE=![]() ×4=4
×4=4![]()
S![]() =
=![]()
∴S![]() = S
= S![]() - S
- S![]() =4
=4![]() -
-![]()

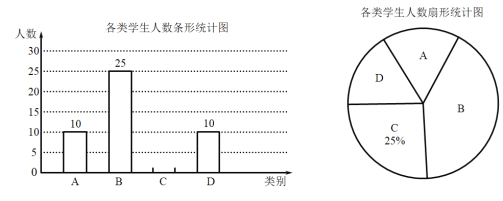
【题目】某超市为了回惯顾客,计划于周年店庆当天举行抽奖活动.凡是购物金额达到m元及以上的顾客,都将获得抽奖机会.规则如下:在一个不透明袋子里装有除数字标记外其它完全相同的4个小球,数字标记分别为“a” 、“b”、“c”、“0” (其中正整数a、b、c满足a+b+c=30且a>15).顾客先随机摸出一球后不放回,再摸出第二球,则两球标记的数字之和为该顾客所获奖励金额(单位:元)、经调查发现,每日前来购物的顾客中,购物金额及人数比例如下表所示:
购物金额x (单位:元) | 0<x<100 | 100≤x<200 | 200≤x<300 | x≥300 |
人数比例 |
|
|
|
|
现预计活动当天购物人数将达到200人.
(1)在活动当天,某顾客获得抽奖机会,试用画树状图或列表的方法,求该顾客获得a元奖励金的概率;
(2)以每位抽奖顾客所获奖励金的平均数为决策依据,超市设定奖励总金额不得超过2000元,且尽可能让更多的顾客参与抽奖活动,问m应定为100元?200元?还是300元?请说明理由.
【题目】为了解某地区企业信息化发展水平,从该地区中随机抽取50家企业调研,针对体现企业信息化发展水平的A和B两项指标进行评估,获得了它们的成绩(十分制),并对数据(成绩)进行整理、描述和分析.下面给出了部分信息.
a.A项指标成绩的频数分布直方图如下(数据分成6组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ):
):
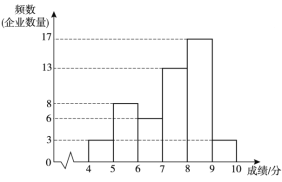
b.A项指标成绩在![]() 这一组的是:
这一组的是:
7.2 7.3 7.5 7.67 7.7 7.71 7.75 7.82 7.86 7.9 7.92 7.93 7.97
c.![]() 两项指标成绩的平均数、中位数、众数如下:
两项指标成绩的平均数、中位数、众数如下:
平均数 | 中位数 | 众数 | |
A项指标成绩 | 7.37 | m | 8.2 |
B项指标成绩 | 7.21 | 7.3 | 8 |
根据以上信息,回答下列问题:
(1)写出表中m的值
(2)在此次调研评估中,某企业A项指标成绩和B项指标成绩都是7.5分,该企业成绩排名更靠前的指标是______________(填“A”或“B”),理由是_____________;
(3)如果该地区有500家企业,估计A项指标成绩超过7.68分的企业数量.