��Ŀ����
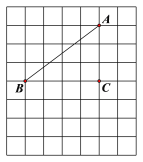
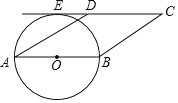
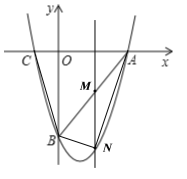
����Ŀ����ͼ�������߹�x��������A��9��0����C����3��0��������y�ύ�ڵ�B��0����12����
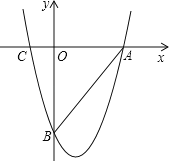
��1���������ߵĽ���ʽ��
��2����MΪ�߶�AB��һ�����㣬����M��MNƽ����y�ύ�������ڵ�N��
���Ƿ���������ĵ�M��ʹ���ı���OMNBǡΪƽ���ı��Σ������ڣ������M�����ꣻ�������ڣ���˵�����ɣ�
�ڵ���M�˶����δ�ʱ���ı���CBNA�������������ʱ��M�����꼰�ı���CBNA��������ֵ��
���𰸡���1��![]() ����2���ٲ����������ĵ�M�����ɼ���������
����2���ٲ����������ĵ�M�����ɼ���������![]() ���ı���CBNA��������ֵΪ
���ı���CBNA��������ֵΪ![]() ��
��
��������
��1���ȸ��ݵ�![]() �������ߵĶ���ʽ���ٽ���
�������ߵĶ���ʽ���ٽ���![]() ������⼴�ɵã�
������⼴�ɵã�
��2���������ֱ��AB�Ľ���ʽ���Ӷ������M��N������ֱ�Ϊ![]() ��
��![]() ���Ӷ��ɵ�
���Ӷ��ɵ�![]() ���ٸ���ƽ���ı��ε����ʿɵ�
���ٸ���ƽ���ı��ε����ʿɵ�![]() ��Ȼ������һԪ���η��̵ĸ����б�ʽ���ɵó��𰸣�
��Ȼ������һԪ���η��̵ĸ����б�ʽ���ɵó��𰸣�
���ȸ��ݵ�![]() ������ֱ����
������ֱ����![]() �ij����ٸ��������������ʽ�����
�ij����ٸ��������������ʽ�����![]() ��������Ӷ��ɵó��ı���CBNA����ı���ʽ��Ȼ�����ö��κ�����������⼴�ɵã�
��������Ӷ��ɵó��ı���CBNA����ı���ʽ��Ȼ�����ö��κ�����������⼴�ɵã�
��1����Ϊ�����߹�x��������![]()
�����������߽���ʽΪ![]()
����![]() ����ã�
����ã�![]()
���![]()
�������߽���ʽΪ![]()
��![]() ��
��
��2����ͼ����ֱ��AB�Ľ���ʽΪ![]()
����![]() ����ã�
����ã�![]() �����
�����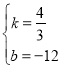
��ֱ��AB�Ľ���ʽΪ![]()
�����⣬�����M������Ϊ![]() ����N������Ϊ
����N������Ϊ![]()
��![]()
�����ı���OMNBΪƽ���ı��Σ���![]()
��![]()
�����ã�![]()
�˷��̵ĸ����б�ʽ![]() ��������ʵ����
��������ʵ����
���������ĵ�M��ʹ���ı���OMNBǡΪƽ���ı��Σ�
��![]()
![]()
![]()
![]()
![]() ��B��MN�ľ������
��B��MN�ľ������![]() ����A��MN�ľ������
����A��MN�ľ������![]()
![]()
![]()
![]()
![]()
��ΪMΪ�߶�AB��һ������
����![]()
�ɶ��κ��������ʿ�֪����![]() ʱ��
ʱ��![]() ��m�����������
��m�����������![]() ʱ��
ʱ��![]() ��m���������С
��m���������С
��![]() ʱ��
ʱ��![]() ȡ�����ֵ�����ֵΪ
ȡ�����ֵ�����ֵΪ![]()
��ʱ��![]()
�ʵ�M������Ϊ![]() ��
��

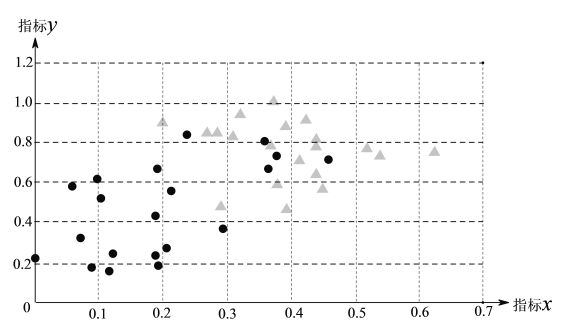
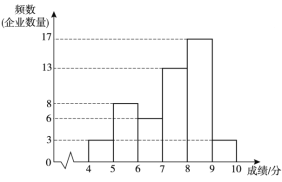
����Ŀ��Ϊ�˽�ij������ҵ��Ϣ����չˮƽ���Ӹõ����������ȡ50����ҵ���У����������ҵ��Ϣ����չˮƽ��A��B����ָ�������������������ǵijɼ���ʮ���ƣ����������ݣ��ɼ������������������ͷ�������������˲�����Ϣ��
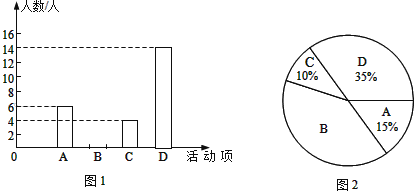
a��A��ָ��ɼ���Ƶ���ֲ�ֱ��ͼ���£����ݷֳ�6�飺![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ����
����
b��A��ָ��ɼ���![]() ��һ����ǣ�
��һ����ǣ�
7.2 7.3 7.5 7.67 7.7 7.71 7.75 7.82 7.86 7.9 7.92 7.93 7.97
c��![]() ����ָ��ɼ���ƽ��������λ�����������£�
����ָ��ɼ���ƽ��������λ�����������£�
ƽ���� | ��λ�� | ���� | |
A��ָ��ɼ� | 7.37 | m | 8.2 |
B��ָ��ɼ� | 7.21 | 7.3 | 8 |
����������Ϣ���ش��������⣺
��1��д������m��ֵ
��2���ڴ˴ε��������У�ij��ҵA��ָ��ɼ���B��ָ��ɼ�����7.5�֣�����ҵ�ɼ���������ǰ��ָ����______________������A������B������������_____________��
��3������õ�����500����ҵ������A��ָ��ɼ�����7.68�ֵ���ҵ������